ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その3
【随時更新】ユークリッド幾何学の定理や作図まとめ - ニート歴10年からの数学日記 を機械的に適用して、解答に至れるかを探る。9月までの方法は全く使わない。定理による確認→(もし発見があれば定理による確認を繰り返し続ける)→作図を1手分で全て試して2通りの意味があるものを発見する→(発見できなければ2手3手と増やしていく)→また定理による確認に戻る、というような手順で行く。
03年度ファイナル問題 問題2
『右の図の四角形ABCDと四角形EFCGは合同な平行四辺形で、辺EGを延長した線は点Dを通り、辺CBを延長した線は点Eを通ります。
このとき、角BACの[ア]倍と角CADの[イ]倍の和は180度となります。
[ア]、[イ]に入る整数をそれぞれ答えなさい。
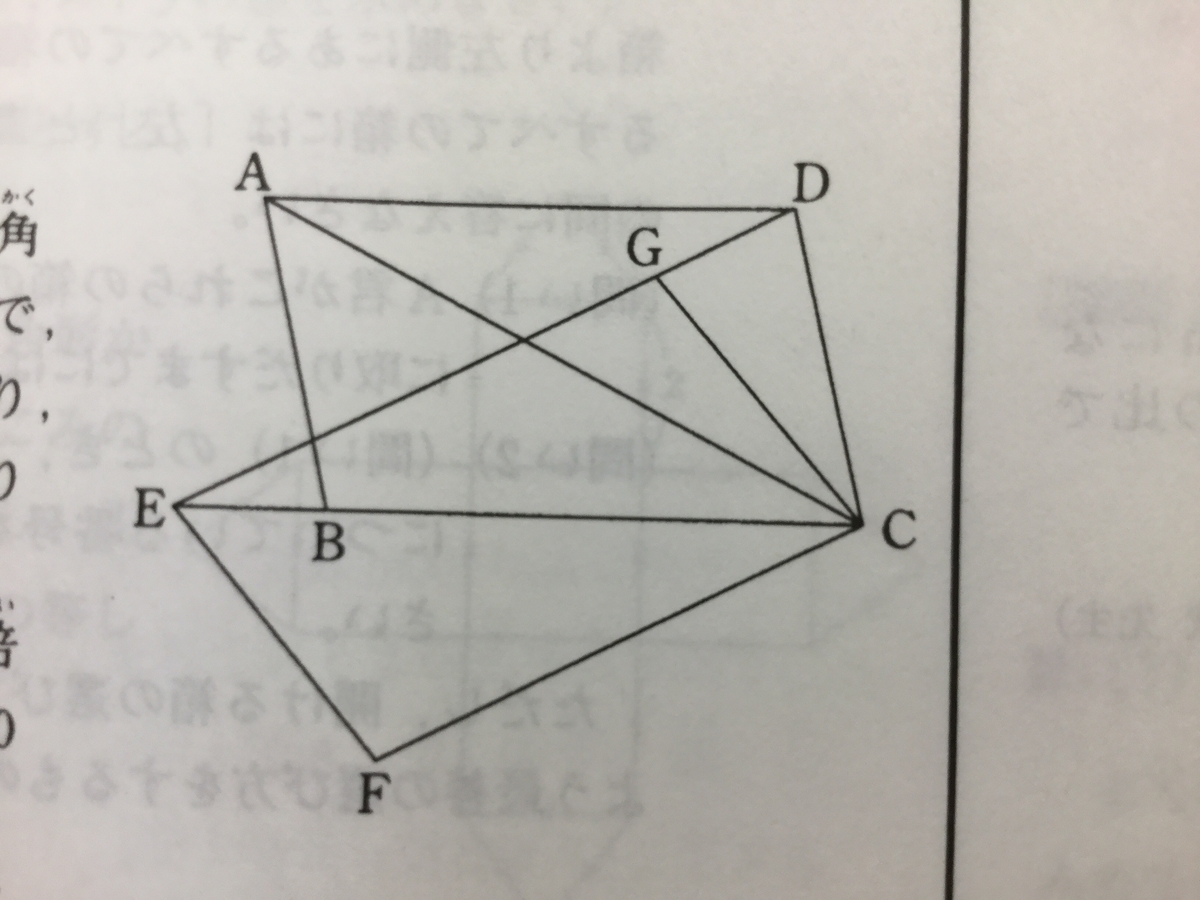 』
』
昨日のやり直し。
まず交点に上からH、Iと名付ける。
平行線と三角形を見つける。ADとECは平行、ABとDCは並行、EDとFCは平行、EFとGCは平行。
三角形は、まずAと繋がっている点を探し、その繋がっている点に更にAと繋がっている点は無いか、アルファベット順にAと繋がっている点を基準にして探していく。
Aと繋がっている点は、点I、B、H、C、D。点BはCと繋がっているか、繋がっている、三角形ABC。Dとは繋がっていない、Hも同じく。Iは直線上なので三角形では無い。点CはDと繋がっていて、三角形ACD。点DはHに繋がっていて、三角形ADH、Iにも繋がっていて、三角形ADI。点HはIと繋がっているので、三角形AHI。ABC、ACD、ADH、ADI、AHI。
Bと繋がっている点は、E、I、(Aは抜かすとして)、C。三角形BEI。
Cと繋がっている点は、F、E、H、G、D。CDE、CDG、CDH、CEF、CEG、CEH、CGH。
Dと繋がっている点は、G、H、I、E。全て同一直線上なので、無し。
Eと繋がっている点は、I、H、G、F。アルファベット順だと、F、G、H、I。無し。
Fと繋がっている点は、CとEを抜かすと無し。
Gと繋がっている点は、HとIだが、これは同一直線上なので、無し。
HとIは、同一直線上だし、そもそももう残り2点なので無視できる。
時間はかかるが、おそらくこれがコンピューター的にもまともな探し方だろう、おそらく。探し直していると時間がかかるので、やはり何かが作図されるたびに、それに関連するものを探すべきだろう。
次に、平行線の同位角と錯角を探す。
平行線ADとECに跨る線は、ADを辿って探すと、AB、AC、DE、DC。
ABは、上の平行線においては右下の角が成立している、下の平行線においては左上と右上の角が成立している。右下の錯角である左上が適合した。∠DAB=∠ABE。
ACは、上の平行線において右下の角が成立している、下の平行線においては左上の角が成立している。右下の錯角は左上なので、∠DAC=∠ACBで、CBを延長するとEがあるので、更に=∠ACE。∠DAC=∠ACB=∠ACE。
DEは、上の平行線においては左下の角が成立している、下の平行線においては右上の角が成立している。左下の錯角は右上なので、∠ADE=∠DEB。更に、EBを延長するとCがあるので、=∠DEC。DEの間にG、H、Iがある。=∠ADG=∠ADH=∠ADI、=∠IEB=∠HEB=∠GEB、=∠IEC=∠HEC=∠GEC。∠ADE=∠DEB=∠DEC=∠ADG=∠ADH=∠ADI=∠IEB=∠HEB=∠GEB=∠IEC=∠HEC=∠GEC。
DCは、上の平行線においては左下の角が成立している、下の平行線においては左上の角が成立している。左下の同位角も錯角も無し。
平行線ABとDCに跨る線は、BC、ID、AC、AD。
BCは、左の平行線においては左上と右上の角が成立している、右の平行線においては左上の角が成立している。左上の同位角は左上なので、まず∠IBE=∠DCB。IBを延長するとAがあるので、=∠ABE。CBを延長するとEがあるので、=∠DCE。∠IBE=∠DCB=∠ABE=∠DCE。
IDは、左の平行線においては左下と右下と右上が、右の平行線においては左下が成立している。左下の同位角は左下なので、∠EIB=∠GDC。GDを延長するとH、I、Eがあるので、=∠HDC=∠IDC=∠EDC。∠EIB=∠GDC=∠HDC=∠IDC=∠EDC。
ACは、左の平行線は右下が成立、右の平行線は左上が成立している。右下の錯角は左上なので、まず∠HAI=∠HCB。AHを延長するとCがあるので、=∠CAI。AIを延長するとBがあるので、=∠HAB。ああ、=∠CABでもあるな。BCを延長するとEがあるので、=∠HCE。HCを延長するとAがあるので、=∠ACB。=∠ACEでもある、か。∠HAI=∠HCB=∠CAI=∠HAB=∠CAB=∠HCE=∠ACB=∠ACE。
ADは、左の平行線では右下が成立、右の平行線では左下が成立。右下の同位角も錯角も無いので終了。(ちょっと休憩)
(よく考えたら一番小さな角だけを明らかにして、大きいというか外側からは一番内側を参照するみたいな話なんだっけ。寝起きだから忘れていた。まあ、途中までやってしまったんで、今回はこれで通してみる。)
平行線EDとFCに跨る線は、EF、EC、HC、GC、DC。
EFは、上の平行線においては右下が、下の平行線においては右上が成立している。だが右下と右上は同位角でも錯角でも無い。
ECは、上の平行線においては右下が、下の平行線においては左上が成立している。右下の錯角は左上なので、まず∠IEB=∠BCF。IEを延長するとH、G、Dがあるので、=∠HEB=∠GEB=∠DEB。更にEBを延長するとCがあって、=∠IEC、しかもそれでもIEを延長すればH、G、Dはあるので、=∠HEC=∠GEC=∠DEC。BCを延長するとEがあるので、=∠ECF。∠IEB=∠BCF=∠HEB=∠GEB=∠DEB=∠IEC=∠HEC=∠GEC=∠DEC=∠ECF。
HCは、上の平行線においては全て成立していて、下の平行線においては左上が成立している。左上と左上は同位角なので、まず∠AHI=∠HCF。HIを延長するとEがあるので、=∠AHE。HCを延長するとAがあるので、=∠ACF。∠AHI=∠HCF=∠AHE=∠ACF。
GCは、上の平行線においては左下と右下が、下の平行線においては左上が成立している。右下の錯角は左上なので、∠DGC=∠GCF。
DCは、上の平行線においては左下が、下の平行線においては左上が成立している。左下の同位角も錯角も無いので、無し。
平行線EFとGCに跨る線は、EG、EC、FC。
EGは、左の平行線においては右下が、右の平行線においては左下が成立している。右下と左下は同位角でも錯角でも無いので、無し。
ECは、左の平行線においては右下が、右の平行線においては左上が成立している。右下と左上は錯角なので、まず∠BEF=∠GCB。EBを延長するとCがあるので、=∠CEF。CBを延長するとEがあるので、=∠GCE。∠BEF=∠GCB=∠CEF=∠GCE。
FCは、左の平行線においては右上が、右の平行線においては左上が成立していて、右上と左上は同位角でも錯角でも無いので、無し。
これで全部か。次は、三角形の内角を確かめよう。具体的な数値が出ないのは予想外だったが、2角が同じであれば、もう1角も等しい。とりあえずキリが良いので休憩しよう。
下に同じ角を書き出してみた。不毛感漂うが、まあゼロから始めたばかりなんで、こんなものだろう。しかし一つ前のは、解答に至る体系性というか理論という意味で、かなり良いものだったと思うんだが、まあ。
∠DAB=∠ABE。
∠DAC=∠ACB=∠ACE。
∠ADE=∠DEB=∠DEC=∠ADG=∠ADH=∠ADI=∠IEB=∠HEB=∠GEB=∠IEC=∠HEC=∠GEC。
∠IBE=∠DCB=∠ABE=∠DCE。
∠EIB=∠GDC=∠HDC=∠IDC=∠EDC=∠AIH=∠AIG=∠AID。
∠HAI=∠HCB=∠CAI=∠HAB=∠CAB=∠HCE=∠ACB=∠ACE。
∠IEB=∠BCF=∠HEB=∠GEB=∠DEB=∠IEC=∠HEC=∠GEC=∠DEC=∠ECF。
∠AHI=∠HCF=∠AHE=∠ACF=∠GHC=∠DHC。
∠DGC=∠GCF。
∠BEF=∠GCB=∠CEF=∠GCE。
三角形も書き出しておく。ってミスってるじゃないか。休憩前に書き直しておく。もし読んでいる人がいるとすれば、書き直されたものを読んでいるはずだ。
ABC、ACD、ADH、ADI、AHI。
BEI。
CDE、CDG、CDH、CEF、CEG、CEH、CGH。
いや待てよ、HとIの錯角が気になるな。例えば∠EIB=角AI?だったりするわけで。いやでも、真ん中にIとかHが入っていて、影響しそうなものは無いな。じゃあ続き。
三角形ABCの内角から調べていく。∠DAC=∠ACB=∠ACE、∠HAI=∠HCB=∠CAI=∠HAB=∠CAB=∠HCE=∠ACB=∠ACE、がマッチ。一方がもう一方にもあれば、2角が等しいわけだから、もう1角も等しいということになる。無いな。∠ACEが両方にあるけど、別に2角が同じというわけでは無いのだし。
三角形ACD。∠DAC=∠ACB=∠ACE。一つだけだから無いな。
ADH。∠ADE=∠DEB=∠DEC=∠ADG=∠ADH=∠ADI=∠IEB=∠HEB=∠GEB=∠IEC=∠HEC=∠GEC。無いな。
ADI。∠ADE=∠DEB=∠DEC=∠ADG=∠ADH=∠ADI=∠IEB=∠HEB=∠GEB=∠IEC=∠HEC=∠GEC。無い。
AHI。∠HAI=∠HCB=∠CAI=∠HAB=∠CAB=∠HCE=∠ACB=∠ACE、∠AHI=∠HCF=∠AHE=∠ACF。一方がもう一方にも無いか、今回は右を基準に確認してみる。無いな。
いや待て、一応錯角も追加しておいた方が良いか。∠EIB=∠GDC=∠HDC=∠IDC=∠EDC=∠AIH=∠AIG=∠AID。∠AHI=∠HCF=∠AHE=∠ACF=∠GHC=∠DHC。
じゃあ、∠GHCと∠DHCでも確認しよう。無いな。今までのも、影響は無さそうだ。
めんどうなんで、オリジナルの方を修正しておく。だから読む人がいるとしたら、上の段落でなぜ抜けてるのかと混乱するだろうな。あと錯角の処理はどうしたとか。直接読むことに意味がある代物では無いし、もし後世に人文学のようなものが残っていてそれで読んでいるのだとしたら、君は何も分かっていないと言っておく。
三角形BEI。∠IBE=∠DCB=∠ABE=∠DCE、∠EIB=∠GDC=∠HDC=∠IDC=∠EDC=∠AIH=∠AIG=∠AID、∠IEB=∠BCF=∠HEB=∠GEB=∠DEB=∠IEC=∠HEC=∠GEC=∠DEC=∠ECF。一番最初ので後の2つを調べて、それから真ん中で右を調べようか。∠DCEと∠EDCと∠DECがマッチした、ということは三角形BEI=三角形CDE。
いや、見逃している。∠ADE=∠DEB=∠DEC=∠ADG=∠ADH=∠ADI=∠IEB=∠HEB=∠GEB=∠IEC=∠HEC=∠GEC、もだ。
ん?∠DEBが被っているぞ?ということは被っている組は全部イコールじゃないか。∠ADIと∠AIDもあるな。
いや三角形BEIとCDEとADIは相似というだけだったか。
もう駄目だ。最後に流れを見直して、仕切り直そう。次は、最小の角を参照するという方法でやりたいが、できるかどうか。
まず、平行線と三角形を見つけておく。対頂角(直線が交わる時に発生する向かい合う角)が発生する交点も見つけておくか?
次に、平行線で、最小の同位角と錯角をイコールで結んでおく。最小の対頂角もイコールで結んでおく。
最小のもので、例えば角X=角Y、角Y=角Z、というようなものがあれば、角X=角Zという風にもしておくか。
で、三角形の内角で、角がイコールなもので、もう一角もイコールじゃないか調べていく、という感じかな。三角形を基準に調べて行けば良い。まあ今日よりはまともになりそうだが。