記述できなかった問題 その4 算数オリンピック 三次元ユークリッド幾何
最後に記述できなかった問題を書き残しておく。
94年度トライアル問題 問題10
『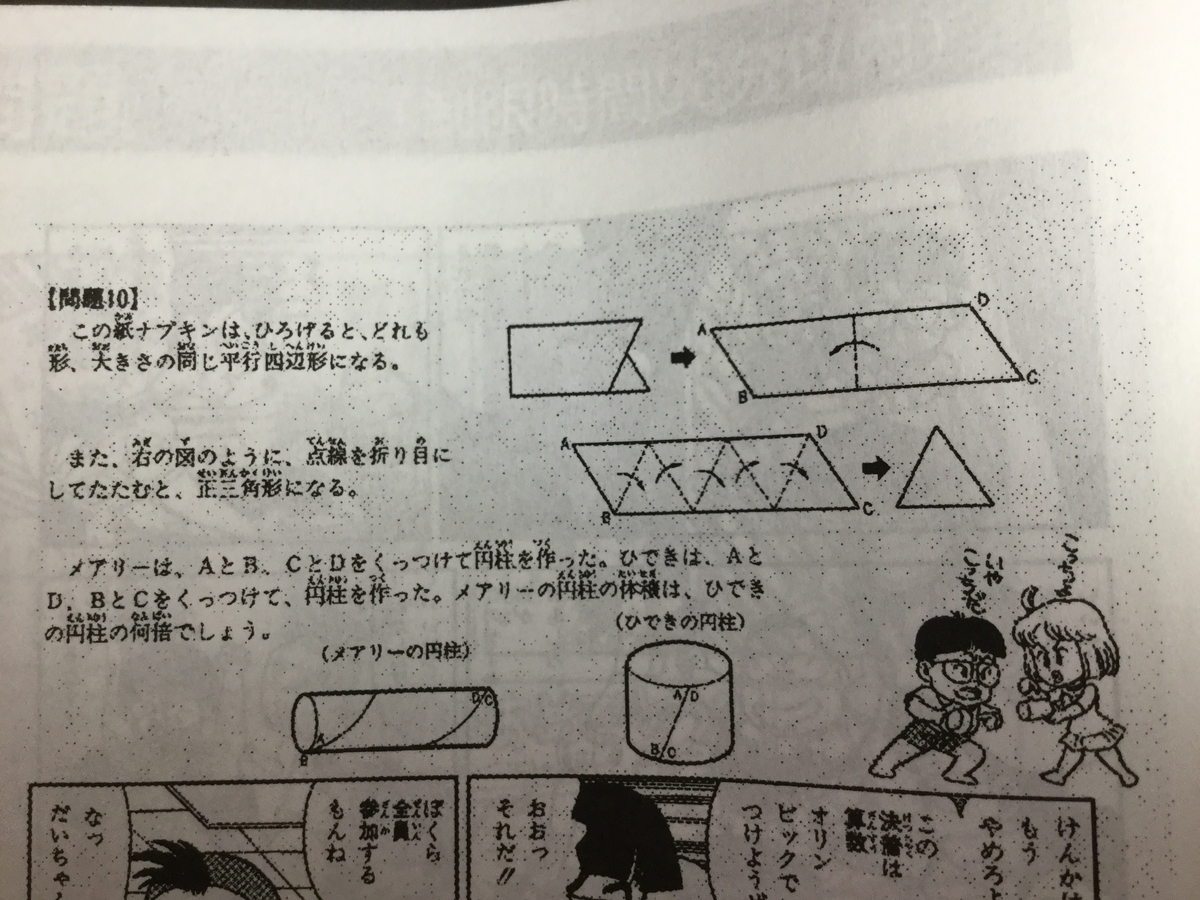 』
』
96年度トライアル問題 問題9
『同じ大きさの立方体27個が、たて3個、横3個、高さ3個にすきまなくぎっしりと並んで大きな立方体の形に積まれています。
細いまっすぐな針金1本で、この大きな立方体をつきさすとき、小さい立方体を最高何個までつらぬくことができますか。
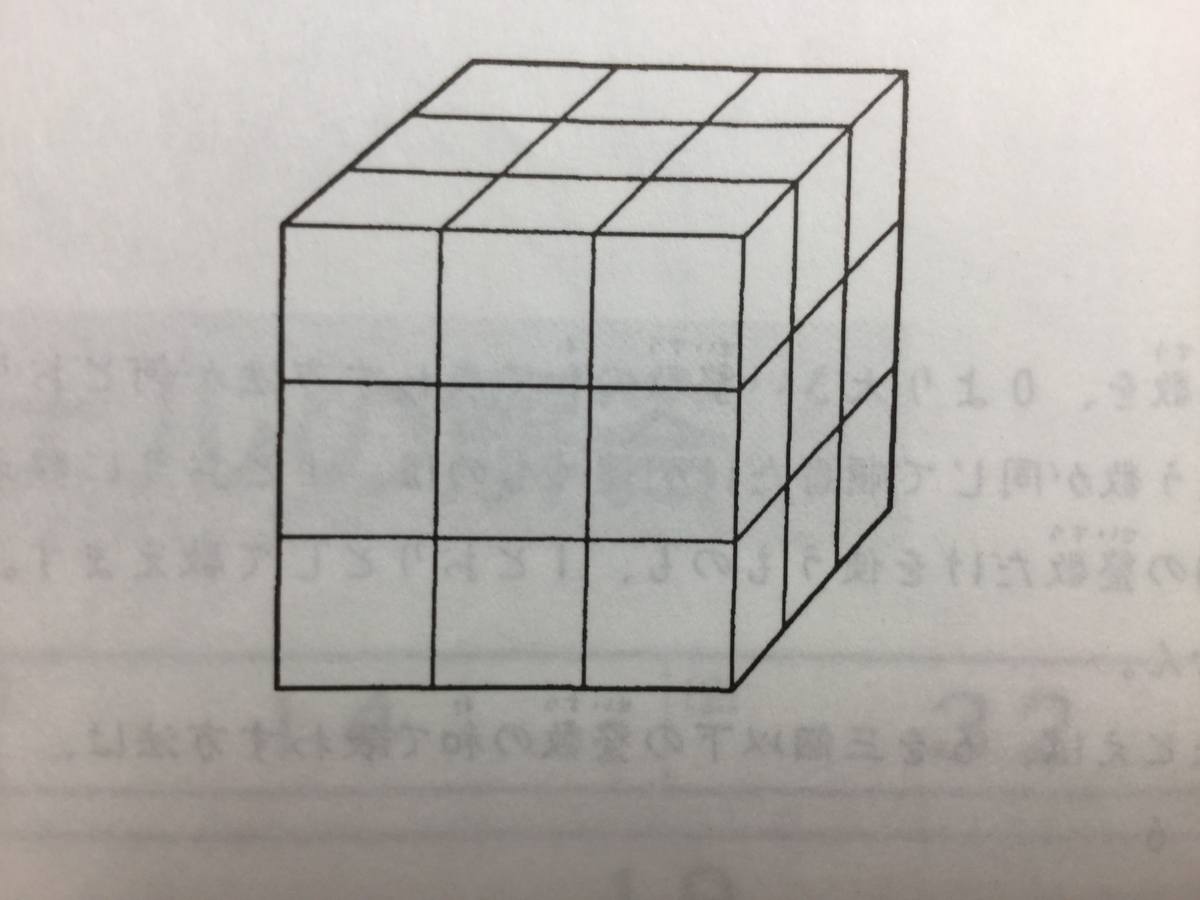 』
』
02年度トライアル問題 問題2
『半径50cm、高さ1mの円形のテーブルに正方形の白い布をかぶせたら、白い布の4つの角が、ちょうどぴったり床につきました。正方形の白い布の面積は何m^2ですか。』
05年度トライアル問題 問題9
『図のようなピラミッドの模型があります。底面は1辺20cmの正方形で、ピラミッドの高さは15cmです。底面の辺BCの延長上、BF=40cmの点Fの真上に光源Pがあります。ピラミッドの影をなくすにはPの高さhを何cm以上にすればよいですか。
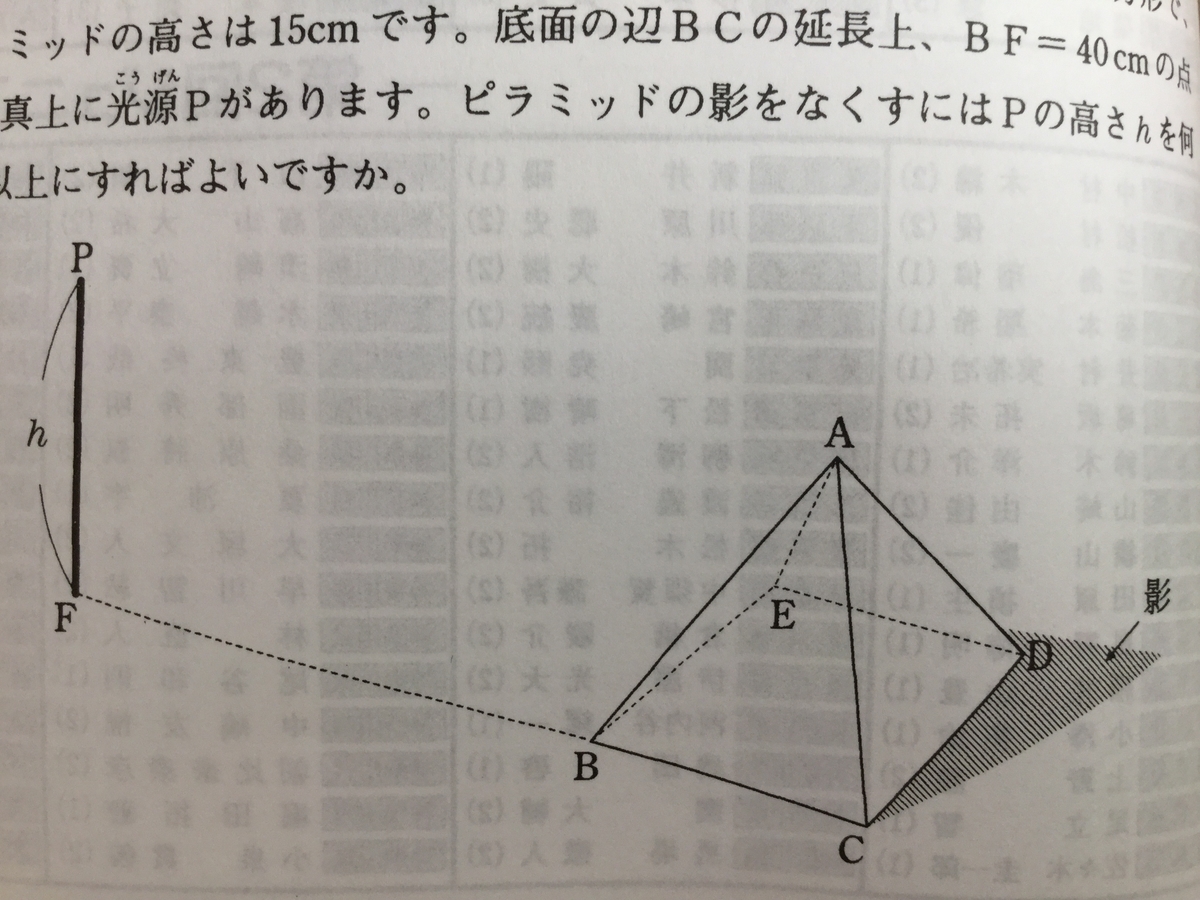 』
』