記述できなかった問題 その8 番外編
最後に記述できなかった問題を書き残しておく。
こういう問題は今まではルールというか関係を数式で表して解いていたけど、もっと違う記述法がある気もするので、一応番外編として載せておく。
算数オリンピック92年度トライアル問題 問題4
『プールの中に立って手のひらで水面をたたくとたたいたところから波が広がっていきます。このような波の速さは、水の深さに関係があります。水の深さがどこも同じなら、立ち止まって作った波も歩きながら作った波も、強くたたいて作った波も、弱くたたいて作った波も、みんな同じ速さで進んでいきます。波とは不思議なものですね。
さて、ある遊園地のプールに、10秒間に6つの波を作る機械が取り付けられています。この機械はプールの底にしかれたレールにそって一定の速さで動かすことができます。また、このプールはどこも同じ深さで、波は10秒に12mの速さで進みます。
またこのとき、波のいちばん高いところを波の山とし、いちばん低いところを波の谷とします。
①この機械が止まったまま波を作っているとき一つの波の山からとなりの波の山までの距離は何mですか。
②太郎君は止まったまま波を作っている機械に向かって、10秒に4mの速さで歩いています。太郎君は10秒にいくつの波の山で出会いますか。時間は、波の谷がちょうど太郎君の位置に来たところから計ることにします。
③今度は止まっている太郎君に向かって、機械が10秒に4mの速さで近づきながら波を作っています。太郎君は10秒間にいくつの波の山に出会いますか。時間は、波の谷がちょうど太郎君の位置に来たところから計ることにします。
④機械と太郎君はそれぞれ10秒に4mの速さで向かいあって進んでいます。太郎君は、10秒間にいくつの波の山に出会いますか。時間は、波の谷がちょうど太郎君の位置に来たところから計ることにします。』
算数オリンピック93年度ファイナル問題 問題3
『平太君が学校から家に帰ろうとすると、1時間に10mmの雨が振っていました。
「1時間に10mmの雨」というのは、平らな地面に置いた円柱の容器に、1時間で10mmの高さまで雨がたまることを表しています。
傘を持って来なかった平太君は、家まで走って帰ろうか、それとも歩いて帰ろうかとなやんでいます。
学校から家までの距離は12km、平太君の走る速さは時速12km、歩く速さは時速4kmです。
また、雨つぶは毎秒1mの速さで地面に垂直に落ちてくるものとし、平太君の体を図のような直方体として計算してみましょう。
平太君が家まで歩いて帰る場合にぬれる量は、走って帰る場合の何倍でしょうか。
 』
』
算数オリンピック94年度トライアル問題 問題1
『お店からここまで、信号は全部450mの間かくでならんでいて、どれも青35秒、黄色5秒、赤35秒のくり返しだ。
ピザ屋のお兄さんは、ずっと時速54kmでバイクを運転して来たので、どの信号も、差しかかった瞬間に青になったそうだ。
同じ道を引き返す時、同様に、どの信号も、差しかかった瞬間に青になるように帰るには、時速何kmでバイクを運転すればいいだろう。もっとも速い速さを考えよう。
 』
』
記述できなかった問題 その7 広中杯
最後に記述できなかった問題を書き残しておく。
- 00年度ファイナル問題 問題4
- 01年度ファイナル問題 問題5
- 03年度ファイナル問題 問題4の1
- 04年度トライアル問題 問題2の3
- 05年度トライアル問題 問題3
- 12年度トライアル問題 問題1の2
00年度ファイナル問題 問題4
『一辺の長さが15の正六角形の板が1枚と半径1の円板がたくさんあります。いま、正六角形の板を机の上に置きそのまわりに半径1の円板を次の条件をみたすように置いていきます。
(ア)板は、重ねて置いてはいけない。
(イ)すべての円板は、正六角形板と1点で接する。(角で接していても良い)
(ウ)隣りあう円板どうしは、接していても接していなくてもよい。
このとき、円板は最大で何枚並べることができますか。
 』
』
01年度ファイナル問題 問題5
『半径2の円板O’上に、中心からの距離が1の定点Pがあります。円板O’を半径4の円Oに内接させながら転がすとき、点Pが動く図形によって囲まれる部分の面積を求めなさい。
 』
』
03年度ファイナル問題 問題4の1
『たとえば、1辺の長さが1の正6角形の各辺の外側に、1辺の長さが1の正6角形を1つずつくっつけると、くっつけた正6角形のとなりあう2つは1辺を共有する。
1辺の長さが1の正m角形の各辺の外側に1辺の長さが1の正n角形を1つずつくっつけたとき、くっつけた正n角形のとなりあう2つが1辺を共有するようなm、nの組として考えられるものをすべて求めなさい。(m,n)=(6,6)のように答えよ。(解答例以外の組を答えなさい。)
 』
』
04年度トライアル問題 問題2の3
『半径1、高さ1の円柱がある。上面の円周の4等分点をA、B、C、D、中心をOとし、ACを含む底面と45°の角をなす平面、およびBDを含む底面と45°の角をなす平面による円柱の側面の切り口を図のようにC1、C2とする。
C1、C2の交点をPとするとき、線分OPの長さを求めよ。
 』
』
05年度トライアル問題 問題3
『互いに交わらない3つの円があるとき、
その3円全てと外接する円を、3円の共通外接円
その3円全てと内接する円を、3円の共通内接円
と呼ぶことにする。(右図参照)

(1)3つの円があり、
・各々の円の半径は1
・3円の中心をA、B、Cとしたとき、AB=3、BC=4、CA=5
であるとする。この3円の共通外接円の半径を求めよ。(答のみで良い)
(2)一辺の長さが8の正三角形XYZがある。
Xを中心とする半径2の円をC1
Yを中心とする半径3の円をC2
Zを中心とする半径4の円をC3
とするとき、C1、C2、C3の共通内接円の半径Rと共通外接円の半径rの差R−rを求めよ。
ただし、C1、C2、C3に、共通内接円、共通外接円がそれぞれただ一つ存在することは、証明無しに用いて良い。
(考え方の欄に途中の考え方を、答の欄に答を記しなさい。途中の考え方も採点対象になります。)』
12年度トライアル問題 問題1の2
『一辺の長さが4で、内角の一つが30°であるひし形がある。このひし形を、ある一辺の周りに1回転させることによってできる立体の体積を求めよ。』
記述できなかった問題 その6 ジュニア広中杯
最後に記述できなかった問題を書き残しておく。
04年度ファイナル問題 問題1
『 』
』
05年度ファイナル問題 問題2の1
『図のように、半径の異なる2つの円C、Dが直線lに接している。C、D、lの全てに接する円はいくつあるか?
ただし、C、Dは共有点を持たず、またC、Dの中心はlに関して同じ側にあるものとする。
(注)2つの円が接するとは、2円が共有点をただ一つ持つことを、円と直線が接するとは、円と直線が共有点をただ一つ持つことをそれぞれ表している。
 』
』
07年度ファイナル問題 問題3
『図1の様に、7×7の正方形のマスと、「マスS」、「マスG」がくっついたものがある。マスは、全て1辺の長さが1の正方形である。
Sの中心からGの中心まで、点Pが全てのマスをちょうど1回ずつ通って移動する。
ただし、Pは水平方向か上下方向にしか移動せず、距離1だけ進むごとにのみ方向を変えることができるものとする。
このときの点Pの軌跡をマスに書き込んだ結果、「まっすぐな線」のみが残っている(マスS、G以外の)マスの個数をXとする。
例えば、図2の様に移動した場合、X=21となる。

(1)X=7となるような点Pの軌跡の例をひとつ、解答欄に記せ。
(2)Xは必ず奇数となることを証明せよ。
(3)Xは5以下となることはない。そのことを証明せよ。』
答えに必要な理由が多分抽象的な問題。
08年度トライアル問題 問題12
『平面上に、異なる8個の点を次の性質を持つように配置できるだろうか?できるならそのような一例を挙げ、説明せよ。できないならその理由を説明せよ。
(性質)8個の点のどの2点を結んでも、その線分の垂直二等分線上に、8個の点のうちの少なくとも2点が存在する。』
この問題もそうなのかな?よく分からないけど。
記述できなかった問題 その5 算数オリンピック その他
最後に記述できなかった問題を書き残しておく。
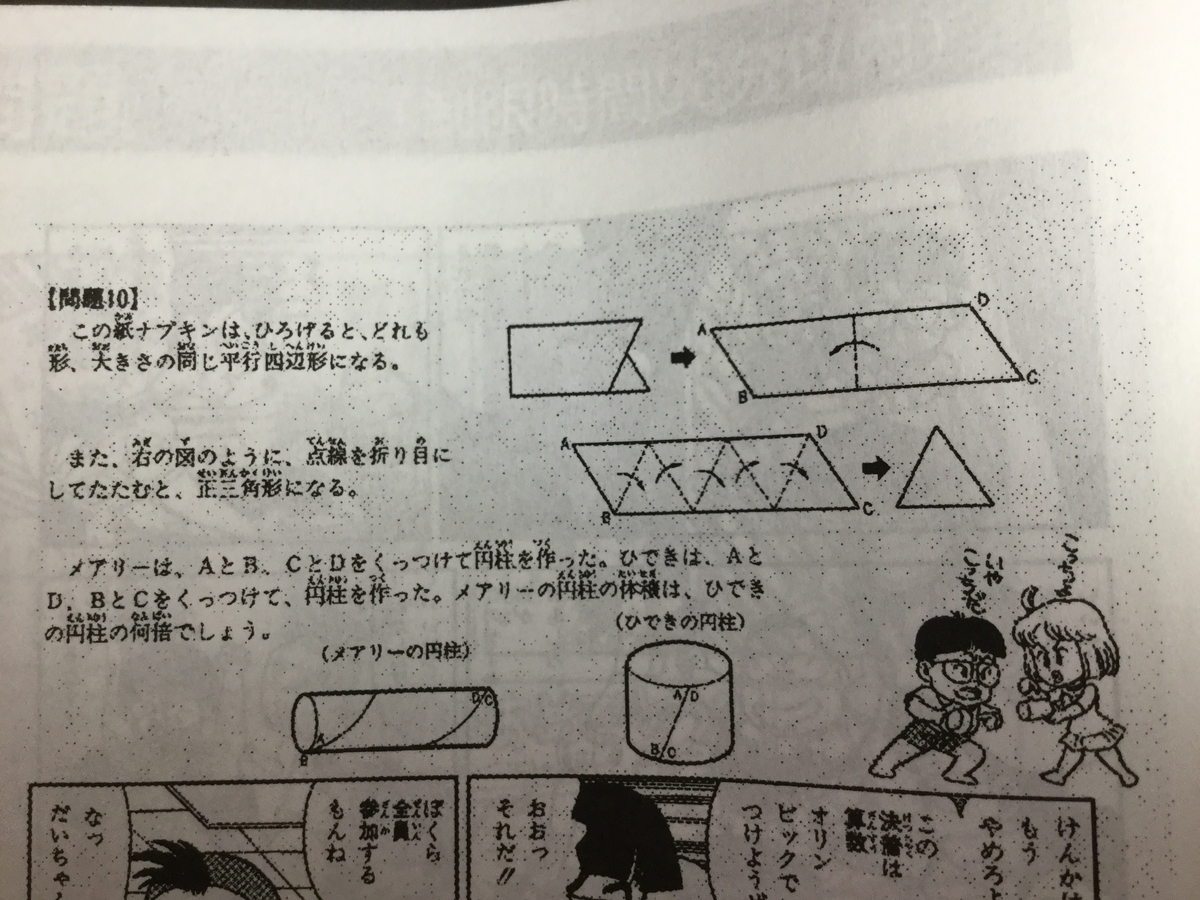
93年度トライアル問題 問題10
『立体の面を、違った色でぬり分ける問題です。自由に曲げたりねじったりすることができる特殊なゴムでできた正三角柱があります(図1)。
これを曲げて、AとD、BとE、CとFが重なって、辺もぴったりと重なるように底面どうしをはり合わせます(図2)。このように、立体をねじらずに曲げて、底面どうしをはり合わせた立体を「基本の形」と呼ぶことにします。
こうしてできた基本の形の面を、つながった面は一つの面だと考えてぬり分けます。すると正三角柱の場合、基本の形の面をぬり分けるのに、3色が必要となります。
今度は、正三角柱が基本の形から、いったん底面をはがして、立体をねじりながら(図3)、底面ABCを120度回転するまで立体をねじって、AとF、BとD、CとEが重なって、辺もぴったりと重なるように、底面どうしをはり合わせます(図4)。これを「基本の形を120度ねじった立体」と呼ぶことにします。
(問い1)正三角柱の場合、基本の形を120度ねじった立体の面をぬり分けるには、何色必要でしょうか。
今度は、同じ材質でできた正四角柱の場合で考えます。基本の形を次のようにねじった立体を作って面をぬり分けるとき、必要な色数を答えなさい。
(問い2)90度ねじった立体では、何色必要ですか。
(問い3)180度ねじった立体では、何色必要ですか。
さらに、同じ材質の正三角柱から正十五角柱まで、13種類の正多角柱を使って、基本の形から、底面どうしの辺や頂点がぴったりと重なるように、いろいろな角度にねじった立体を作って、面をぬり分けます。それぞれの正多角柱の場合の、ぬり分けるのに必要な色の数の種類について、下の問いに答えなさい。
(例えば、基本の形が4色必要で、ねじった立体では、必要な色の数が1色、2色をくりかえすような正多角柱の場合、必要な色の数の種類は3種類となります。)
(問い4)ぬり分けるのに必要な色の数の種類が、もっとも多いのは正何角柱の場合でしょうか。
(問い5)ぬり分けるのに必要な色の数の種類が、基本の形も含めて2種類しかないものは、正何角柱の場合でしょうか。すべて答えなさい。
 』
』
96年度ファイナル問題 問題1
『人口1000人の村に1000軒の家があり、村の人はみんな一人で住んでいます。この村では、お正月にすべての村の人が、自分の家からいちばん近い距離にある家に1枚だけ年賀状を出します。家どうしの距離はみんな違います。また、村の外から年賀状は来ません。
さて、この村では、一人の村の人が最高で何枚の年賀状をもらえますか。その理由も答えなさい。』
こういう問題は実は本質的な課題だという気がする。
96年度ファイナル問題 問題5
『円周上に点がいくつかならんでいます。これらの点を一つおきに直線でつないでいったところ、すべての点を通って、はじめの点にもどりました。こうしてできた図形のとがった部分の角度(図の黒い角の部分)の合計は2700度でした。
円周上に点はいくつありますか。
 』
』
99年度ファイナル問題 問題2
『端に火をつけると、ちょうど8分で燃えつきるロープが何本もあります。このロープを使って時間がはかれます。
たとえば、1本のロープの両方の端に同時に火をつけると燃えつきるまでに4分。1本のロープの一方の端に火をつけ、燃えつきると同時に次のロープの一方の端に火をつけると16分がはかれます。
では、下のルールのもとに、6分、7分、9分、10分、11分、12分をそれぞれはかることができるでしょうか。はかれるものには○、はかれないものには×を回答欄につけなさい。
ルール1:使えるロープは1つの時間をはかるのに3本以内とする。
2:火を付けるのはロープの端だけ。
3:同時に火を付けるのは何箇所でも良い。
4:火は途中で消せない。
5:ロープを切ったり、折ったりしてはいけない。』
06年度トライアル問題 問題11
『1枚の紙の上に何個かの点があるとき、以下のルールにしたがって点と点をまっすぐな線で結びます。
ルール1)どの点も最低1個のほかの点と結ばれるようにする。
ルール2)線どうしは交わらないようにする。
このとき、線でかこまれた部分を「区域」とよび、その個数を数えます。
たとえば6個の点があるとき、(図1)や(図2)の場合は3個、(図3)の場合は4個の区域があることになります。

いま、1枚の紙の上に2006個の点があり、これらの点どうしをルールにしたがってまっすぐな線で結んで2006個の区域を作るとき、最小で何本の線を引いたらよいですか。
ただし、どの線も必ず区域をかこんでいるものとします。』
これも本質的な課題で、答えに必要な理由がなんか抽象的な気がする。
記述できなかった問題 その4 算数オリンピック 三次元ユークリッド幾何
最後に記述できなかった問題を書き残しておく。
94年度トライアル問題 問題10
『 』
』
96年度トライアル問題 問題9
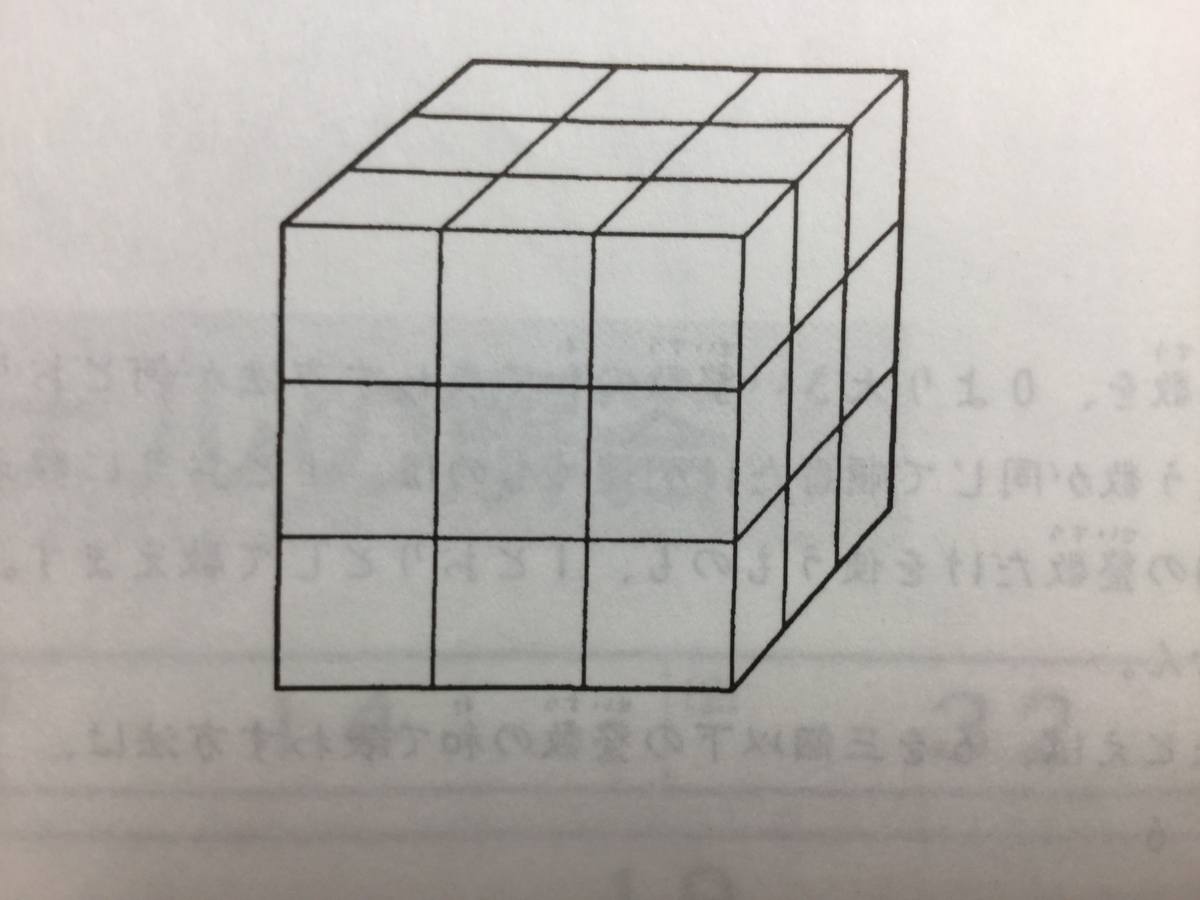
『同じ大きさの立方体27個が、たて3個、横3個、高さ3個にすきまなくぎっしりと並んで大きな立方体の形に積まれています。
細いまっすぐな針金1本で、この大きな立方体をつきさすとき、小さい立方体を最高何個までつらぬくことができますか。
 』
』
02年度トライアル問題 問題2
『半径50cm、高さ1mの円形のテーブルに正方形の白い布をかぶせたら、白い布の4つの角が、ちょうどぴったり床につきました。正方形の白い布の面積は何m^2ですか。』
05年度トライアル問題 問題9
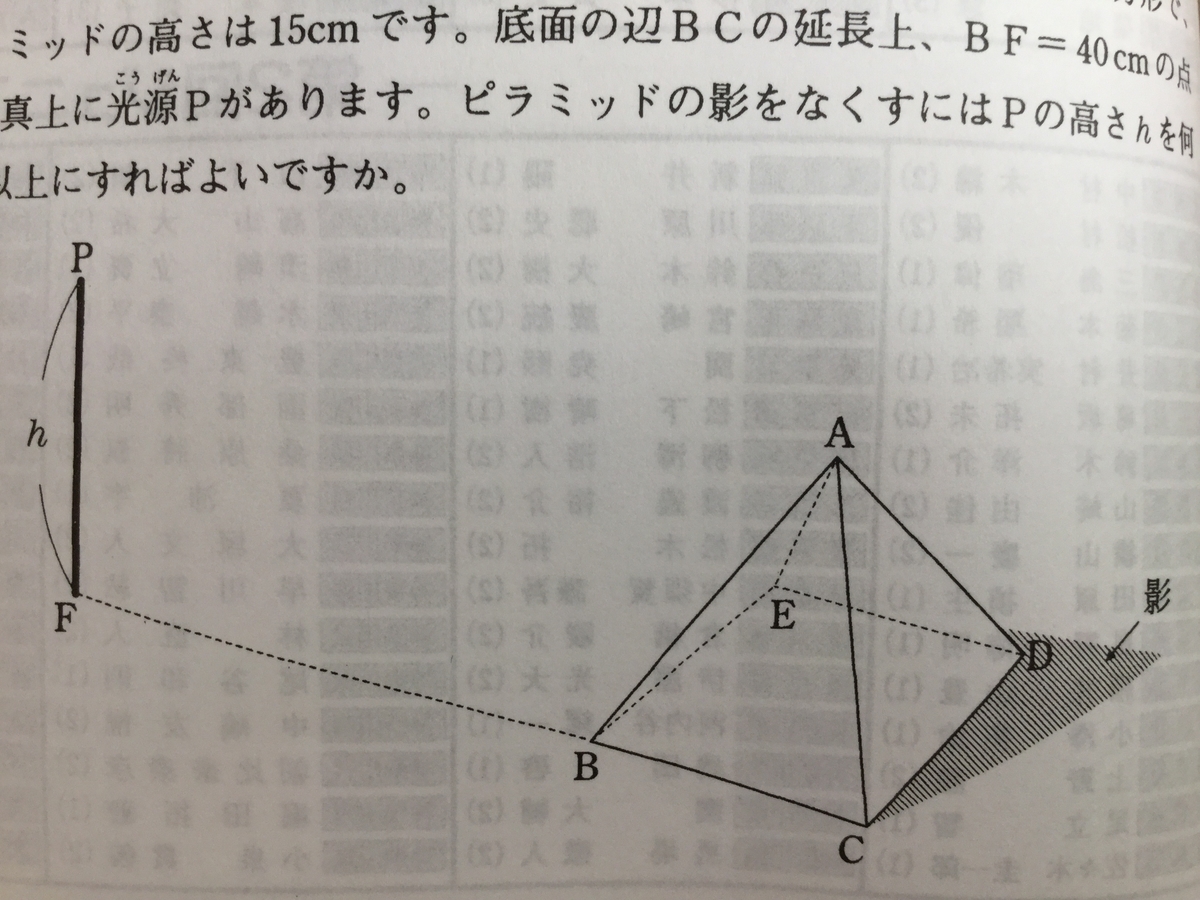
『図のようなピラミッドの模型があります。底面は1辺20cmの正方形で、ピラミッドの高さは15cmです。底面の辺BCの延長上、BF=40cmの点Fの真上に光源Pがあります。ピラミッドの影をなくすにはPの高さhを何cm以上にすればよいですか。
 』
』
記述できなかった問題 その3 算数オリンピック 二次元ユークリッド幾何
最後に記述できなかった問題を書き残しておく。
動きを定義すれば不可能では無いだろう。
最後の問題は、答えを見ると辺と面積の割合の法則で、たしか同じ長さの底辺を底辺における逆側に作図する、みたいな変な作図があった。答えを見るとこういう新しい作図が必要な問題は他にもあるかもしれない。
そういえばだけど、あの中点の作図は、作図の種類に加えることにした。
93年度トライアル問題 問題7
『右の図のように、半径4cmの円の中で、2本の直線が垂直に交わっています。
円の中の、ななめの線が引かれた部分Aの面積と、その他の部分Bの面積では、どちらがどれだけ大きいですか。記号と数字で答えなさい。
 』
』
98年度トライアル問題 問題7
『コンパスの足の幅を2cm開いて、図1のような図形を作ります。
このような図形を2つ用意します。一つの図形は固定され、もう一つの図形はその周囲をすべることなく転がりながら移動していきます。
初めに図2のように頂点が接した状態から転がしていくとき、移動する図形の通過した部分の面積は何cm^2になりますか。円周率は3.14とします。
 』
』
98年度ファイナル問題 問題7
『三角形ABCを三角形A'B'C'の位置まですべることなく転がしました。
このとき三角形ABCが通った範囲の面積を求めなさい。
円周率は3.14とします。
 』
』
10年度トライアル問題 問題12
『三角形ABCのCA上にAE=BCとなるようにEをとります。
さらに、ECの真ん中の点をDとしたとき、BD=15cm、角DBC=15°、角ADB=135°でした。
このとき、三角形ABCの面積を求めなさい。
 』
』
記述できなかった問題 その2 ジュニア算数オリンピック 折る二次元ユークリッド幾何
最後に記述できなかった問題を書き残しておく。
この問題も、動きを定義すれば不可能では無いだろう。
97年度トライアル問題 問題7
『1枚の円形の紙を、直径を折り目にして半分に折り、もう一度ふちがぴったりとそろうように半分に折ります。

(問い1)アのように2本の点線にそって切ると、紙は何枚に分かれますか。
(問い2)イのように2本の点線にそって切ると、紙は何枚に分かれますか。
(問い3)ウのように2本の点線にそって切ると、紙は何枚に分かれますか。』
98年度ファイナル問題 問題7
『図1のように1辺15cmの正三角形に、1辺1cmの正三角形にすべて分ける線が書かれています。この線にそって1辺15cmの正三角形を折ることをくり返し(どのような順番で折ってもかまいません)、図2のような1辺1cmの正三角形にします。
ただし、紙の厚さは考えないものとします。

(問い1)図3のようにこの1辺1cmの正三角形の1つの辺の一部を切りおとしたあと広げるとすると、もとの1辺15cmの正三角形の内部にはいくつの穴があいていますか。(ここで正三角形の内部の穴とは、図5のようにもとの1辺15cmの正三角形の周上の切りおとされた部分は含みません)。
(問い2)今度は図4のように1辺1cmの正三角形の3つの頂点のうちの1つを切りおとしたあと広げるとするともとの1辺15cmの正三角形の内部にはいくつの穴があいていますか。考えられる穴の数をすべて答えなさい。(ここでも内部の穴とは、問い1と同様にもとの1辺15cmの正三角形の周上の切りおとされた部分は含みません)。』
03年度トライアル問題 問題4
『正方形に折り目(図の点線)をつけ、図のようにア〜クの同じ大きさの8つの部分に分けます。折り目のどれかを1回だけ折ったとき、図のキの部分と重なる部分の記号をすべて書きなさい。
 』
』
03年度トライアル問題 問題15
『長さ800cm、幅1cmの紙テープがあります。この紙テープを半分に折り、さらに半分に折り、さらに半分に折り、さらに半分に折りました。
すると、長さ50cm、幅1cmの折りたたまれた紙テープになります。これを端から1cmきざみで、ハサミをつかって切っていきます。全部切り終わると、たくさんの正方形の紙と、何枚かの長方形の紙ができます。さて、正方形の紙は全部で何枚できますか。』