ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その27
グラフで表現したユークリッド幾何学の自動解答に挑戦している。
08年度ファイナル問題 問題12
『(せめて画像だけにしようと思っていたのだけど、ちょっとサイズ的に。二回書くのも何なので問題文は省略)
 』
』
今回は2つあるわけだけど、大丈夫かな。では初期条件。
graph := [
A : [
[[B], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
];
clockwise_lst := [
A : [
[C, [], [], [B]],
[B, [C], [], []],
~
]
,
B : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
];
angle_lst := [
A : [
[
[C, [], [], [B]],
[B, [C], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C],
[D, E, F]
];
triangle_lst := [
];
cluster_lst := [
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
}
辺による辺の和も180°の角の和も無し。angle_lstによる角の和も無し。平行線も無し。
graphを辿って、△ABCと△DEF。clusterも更新。
graph := [
A : [
[[B], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
];
clockwise_lst := [
A : [
[C, [], [], [B]],
[B, [C], [], []],
~
]
,
B : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
];
angle_lst := [
A : [
[
[C, [], [], [B]],
[B, [C], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
}
作図
セットアップが終わったので、作図に移る。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その25 - ニート歴10年からの数学日記、
セットアップ時の角の和の取得法について - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その21 - ニート歴10年からの数学日記の後半、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その18 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その17 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その16 - ニート歴10年からの数学日記、
辺りを参考にしようかな、後ろに行くほどもう参考にならないと思うけど。
- ?正四角形の判定
- ?正五角形の判定
まず点と点を結ぶ所から。手順に慣れるために、前回と同じでも繰り返そうと思う。
って、繋がってない点と点が今は無いのか。
じゃあ次、線を同じ分だけ延長。
graphのAの一番最初のBの反対側に、Gを追加しよう。
AB == AG。かつangle関係も更新する。平面リストにも追加する必要があるんだな。
angle_lstでは、AにおいてBが端っこにある角があれば、その反対側に追加する。角の間にある場合は、つまり角が全部で180°を超えるということになるので、新しく作成を模索する必要があるが、今回は無い。
graph := [
A : [
[[B], [], [G]],
[[C], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
,
G : [
[[A, B], [], []]
]
];
clockwise_lst := [
A : [
[G, [], [], [C, B]]
[C, [G], [], [B]],
[B, [C, G], [], []],
~
]
,
B : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
,
G : [
[A, [], [], []],
~
]
];
angle_lst := [
A : [
[
[G, [], [], [C, B]]
[C, [G], [], [B]],
[B, [C, G], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
,
G : [
[
[A, [], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, G],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
AB == AG;
}
graphから辺の和と180度の角の和を取得。
AB + AG == BG;
BAC_p + CAG_p == BAG_h;
angle_lstから角の和を取得。
CAG_p + BAC_p == BAG_h; #あー、180度の時ってどうしよう
交点はACを基準に調べることになるだろう。angle_lstのAにおいてGはCの上にある。しかしangle_lstのCにおいてAの下には何も無い。なので、ACを基準に三角関数で調べられるような辺のセットは無いと分かる。
やることと言えば、最初の手順みたいなのと、交点の発見と、辺や角において順番が不確定なものの確定と、ぐらいだっけか?(セットアップ時の角の和の取得法について - ニート歴10年からの数学日記の後半参照)
じゃあとりあえず結果を表示して次の作図に行こうか。
graph := [
A : [
[[B], [], [G]],
[[C], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
,
G : [
[[A, B], [], []]
]
];
clockwise_lst := [
A : [
[G, [], [], [C, B]]
[C, [G], [], [B]],
[B, [C, G], [], []],
~
]
,
B : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
,
G : [
[A, [], [], []],
~
]
];
angle_lst := [
A : [
[
[G, [], [], [C, B]]
[C, [G], [], [B]],
[B, [C, G], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
,
G : [
[
[A, [], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, G],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
AB == AG;
AB + AG == BG;
BAC_p + CAG_p == BAG_h;
}
じゃあリセットして次の種類の作図。
次の作図は二等辺三角形の作図で、三角形の内部でのみ作ることにしていて、二種類ともどちらの辺と作るかは角度で決めているのだけど、しかし角度がイコールな場合はどちらの作図もできないんだな。新しい発見だった。
あー、一番最初に三角形定理ループを回すのを忘れてるな。まあ良いか。
いや待てよ。話は戻るが、一番最初の作図は、例えばAとDを結んだりもできたんじゃないか?
いや、でも理想としてはやりたくないんだよな。というのも、全然違う空間にある三角形同士なのだし。
同一平面上にある点同士に限るのは極端だろうか。しかし辺を辿って繋がっている点を保持するリストなんて余計なものは、作りたく無いしなあ。
まあ今回は、考察自体を保留としようかな。できれば省きたいんだが、どうやって省くかというのは。
じゃあ次、リセットしてから、クラスタの接続。クラスタの同じ長さの辺を繋ぐ。
今回はABかACにEFを繋ぐ。どっちにどう繋いでも、それで答えまで行くはずだが。
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]]
];三角形ABCのABに、複製したDEFのEFを繋ぐことにしよう。AにEを、BにFを対応させる。複製した元々Dだった点は、Gと名付けることにしよう。
と思ったのだけど、時計回りを保持したほうが良いのが分かったので、AにFを、BにEを対応させることにした。
[[G, B, A], [AGB_p, BG, ABG_p, AB, BAG_p, AG]]
EDF_p == AGB_p;
DE == BG;
DEF_p == ABG_p;
EF == AB;
DFE_p == BAG_p;
EF == AG;
という感じにしたい。
angle_lstについて、とりあえずはこの上が下になるはず。
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
G : [
[
[A, [], [], [B]],
[B, [A], [], []]
]
]
,
B : [
[
[G, [], [], [A]],
[A, [G], [], []]
]
]
,
A : [
[
[B, [], [], [G]],
[G, [B], [], []]
]
]
それで、繋げた角が180°以下だと判定される前はこう。
graph := [
A : [
[[B], [], []],
[[C], [], []],
[[G], [], []]
]
,
B : [
[[G], [], []],
[[A], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
,
G : [
[[A], [], []],
[[B], [], []]
]
];
clockwise_lst := [
A : [
[C, [], [], [B, G]],
[B, [C], [], [G]],
[G, [B, C], [], []]
~
]
,
B : [
[G, [], [], [A, C]],
[A, [G], [], [C]],
[C, [A, G], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
,
G : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
];
angle_lst := [
A : [
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [G]],
[G, [B], [], []]
]
]
,
B : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
,
[
[G, [], [], [A]],
[A, [G], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
,
G : [
[
[A, [], [], [B]],
[B, [A], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, G],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]],
[[G, B, A], [AGB_p, BG, ABG_p, AB, BAG_p, AG]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
EDF_p == AGB_p;
DE == BG;
DEF_p == ABG_p;
EF == AB;
DFE_p == BAG_p;
EF == AG;
}
で、どちらも180°以下(一方はちょうど180°)なので、こうなる。
結果的に、graphをAのを直線に直した、angle_lstを統合した、クラスタを追加した。
いや、ああでも、Eの角は同じ大きさのが2つあるから90°以下で、だからその半分が加わっても180°以下か。結構しっかりした以上以下の演算が必要で、だからやっぱり自動化は無理なんだろうな。三角関数の関数はあるだろうから、良さそうなソルバー(制約プログラミング言語では無い純粋な解答プログラム)さえ見つかれば、自動化できるのかもしれないけど。
graph := [
A : [
[[B], [], []],
[[C], [], [G]]
]
,
B : [
[[G], [], []]
[[A], [], []],
[[C], [], []]
]
,
C : [
[[A], [], []],
[[B], [], []]
]
,
D : [
[[E], [], []],
[[F], [], []]
]
,
E : [
[[D], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
,
G : [
[[A], [], []],
[[B], [], []]
]
];
clockwise_lst := [
A : [
[C, [], [], [B, G]],
[B, [C], [], [G]],
[G, [B, C], [], []]
~
]
,
B : [
[G, [], [], [A, C]],
[A, [G], [], [C]],
[C, [A, G], [], []],
~
]
,
C : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
,
D : [
[F, [], [], [E]],
[E, [F], [], []],
~
]
,
E : [
[D, [], [], [F]],
[F, [D], [], []],
~
]
,
F : [
[E, [], [], [D]],
[D, [E], [], []],
~
]
,
G : [
[B, [], [], [A]],
[A, [B], [], []],
~
]
];
angle_lst := [
A : [
[
[C, [], [], [B, G]],
[B, [C], [], [G]],
[G, [B, C], [], []]
]
]
,
B : [
[
[G, [], [], [A, C]],
[A, [G], [], [C]],
[C, [A, G], [], []]
]
]
,
C : [
[
[B, [], [], [A]],
[A, [B], [], []]
]
]
,
D : [
[
[F, [], [], [E]],
[E, [F], [], []]
]
]
,
E : [
[
[D, [], [], [F]],
[F, [D], [], []]
]
]
,
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
,
G : [
[
[A, [], [], [B]],
[B, [A], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, G],
[D, E, F]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△DEF : [EDF_p, DE, DEF_p, EF, DFE_p, EF]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[D, E, F], [EDF_p, DE, DEF_p, EF, DFE_p, EF]],
[[G, B, A], [AGB_p, BG, ABG_p, AB, BAG_p, AG]],
[[A, G, B, C], [CAG_p, AG, AGB_p, BG, CBG_p, BC, ACB_p, AC]]
];
always {
AB == AC == EF;
DE == DF;
BC == AB + DE;
DEF_p == ABC_p * 2;
EDF_p == AGB_p;
DE == BG;
DEF_p == ABG_p;
EF == AB;
DFE_p == BAG_p;
EF == AG;
}
よく分からないけど、これで答えまで行くはずなんだけど。こんなんで良いのかな。次回はまた別の問題で可能か探ってみるけど。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26
ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。交点の確認はこの方法を使う。
06年度トライアル問題 問題9
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
 』
』
初期条件。いろいろ増えてしまったけど、必要な気がしている。
graph := [
A : [
[[B], [], []],
[[D], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []]
]
];
clockwise_lst := [
A : [
[B, [], [], [D]],
[D, [B], [], []],
~ #循環リストをこう表すことにした。[X, Y, Z, ~]
]
,
B : [
[C, [], [], [A]],
[A, [C], [], []],
~
]
,
C : [
[D, [], [], [B]],
[B, [D], [], []],
~
]
,
D : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
];
angle_lst := [
A : [
[
[B, [], [], [D]],
[D, [B], [], []]
]
]
,
B : [
[
[C, [], [], [A]],
[A, [C], [], []]
]
]
,
C : [
[
[D, [], [], [B]],
[B, [D], [], []]
]
]
,
D : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, D]
];
triangle_lst := [
];
always {
ABC_p == 168;
BCD_p == 108;
AB == BC == CD;
}
辺による辺の和も180°の角の和も無し。angle_lstによる角の和も無し。平行線も無し。graphを辿っても三角形は見つからない。
作図
セットアップが終わったので、作図に移る。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その25 - ニート歴10年からの数学日記、
セットアップ時の角の和の取得法について - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その21 - ニート歴10年からの数学日記の後半、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その18 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その17 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その16 - ニート歴10年からの数学日記、
辺りを参考にしようかな、後ろに行くほどもう参考にならないと思うけど。
- ?正四角形の判定
- ?正五角形の判定
まず点と点を結ぶ所から。
graphの最初のAを確認して、graphの繋がっていないCと単純に繋げる。clockwise_lstや、angle_lstも更新しなければならない。
まずgraphを更新する。
clockwise_lstのAにおいて、新しく作るCはどこに入るのか。
予想に反して、BとDの両方を問わなければいけないのかな?循環リストだから、2番目か3番目のどちらかなのだけど。
angle_lstなら、Bを問うだけで良いと思うんだけどな。
Aの所にCを追加する時に、AとCでBを共有していて(AにおいてBが通る辺のどれかの点がCと繋がっていたり、CにおいてBが通る辺のどれかの点がAと繋がっているのでも本当は良いと思うのだけど)、angle_lstのBにおいて時計回りでCからAなんで、Aから見てCはBより時計が進んだ側にある(手元で図を描いて理解している)、と言えるのではないか。
更にDに着目すると、時計回りでAからCなんで、Aから見てCはDより時計が戻った側にある。
よって、angle_lstのAにおいて、B、C、Dの順番なはずだ。Cにおいては逆のこと、つまりD、C、Bが言えるはずだ。
clockwise_lstもそれに合わせて更新しておこうか?なんかまだ洗練されてないけど。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[A], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []]
]
];
clockwise_lst := [
A : [
[B, [], [], [C, D]],
[C, [B], [], [D]],
[D, [B, C], [], []],
~ #循環リストをこう表すことにした。[X, Y, Z, ~]
]
,
B : [
[C, [], [], [A]],
[A, [C], [], []],
~
]
,
C : [
[D, [], [], [B, A]],
[A, [D], [], [B]],
[B, [D, A], [], []],
~
]
,
D : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
];
angle_lst := [
A : [
[
[B, [], [], [C, D]],
[C, [B], [], [D]],
[D, [B, C], [], []]
]
]
,
B : [
[
[C, [], [], [A]],
[A, [C], [], []]
]
]
,
C : [
[
[D, [], [], [B, A]],
[A, [D], [], [B]],
[B, [D, A], [], []]
]
]
,
D : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, D]
];
triangle_lst := [
];
always {
ABC_p == 168;
BCD_p == 108;
AB == BC == CD;
}
で、どういう順番で調べていけば良いのかっていうのが分からないというか、模索中で。
まあ、angle_lstから、
BAC_p + CAD_p == BAD_p;
ACD_p + ACB_p == BCD_p;
(angle_lstの角が最大のポジティブなら、その反転側は最小のネガティブなはずで、その最小のネガティブとそれぞれの角を足したのも登録すべきだった)
graphから△ABCと△ACDは言えると思うけど。
辺の和とか180°の角の和とか、平行線は無いし。
そのまま三角形定理ループにかけたら(三角形定理ループで条件が明らかになったらそのままオートで三角関数にもかけるんで)答えが出ちゃうわけだけど。
辺ACを基準に、angle_lstのAの中のCと、Cの中のAで、Bの位置が逆同士なんで三角関数にかけれる(しかしもう三角形として見つかっているのでかけない)とか、そういう判断もあるんだろうか。
次の作図に行くことにしよう。
次は線を同じ分だけ延長しよう。作図はリセットする。
graphを最初から見ていって、Aの1番目を延長する。Bの逆側に新しいEを加える。AB == AEもalwaysに加える。
更にangle_lstのAの、上だろうが下だろうが一番端がBの角があれば、逆側にEを加える。clockwise_lstを更新する。またそれぞれにEも加える。
graph := [
A : [
[[B], [], [E]],
[[D], [], []]
]
,
B : [
[[A, E], [], []],
[[C], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []]
]
,
E : [
[[A, B], [], []]
]
];
clockwise_lst := [
A : [
[B, [], [], [D, E]],
[D, [B], [], [E]],
[E, [B, D], [], []]
~ #循環リストをこう表すことにした。[X, Y, Z, ~]
]
,
B : [
[C, [], [], [A]],
[A, [C], [], []],
~
]
,
C : [
[D, [], [], [B]],
[B, [D], [], []],
~
]
,
D : [
[A, [], [], [C]],
[C, [A], [], []],
~
]
,
E : [
[A, [], [], []]
]
];
angle_lst := [
A : [
[
[B, [], [], [D, E]],
[D, [B], [], [E]],
[E, [B, D], [], []]
]
]
,
B : [
[
[C, [], [], [A]],
[A, [C], [], []]
]
]
,
C : [
[
[D, [], [], [B]],
[B, [D], [], []]
]
]
,
D : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
]
,
E : [
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, D]
];
triangle_lst := [
];
always {
ABC_p == 168;
BCD_p == 108;
AB == BC == CD;
AB == AE;
}
模索中だが、辺の和と180°の角の和を更新する。
AB + AE == BE
BAD_p + DAE_p == BAE_h
Eに繋がっている辺はAE以外に無いから三角関数は無理で、AからはBへは直線で、ADで調べることになるだろう。AとDを基準に、しかしangle_lstのDの中のAより上には何も無いので、何も無し。
ああ後、coplanar_lstにもEを追加するんだった。
こんな感じだろうか。次の作図に行こう。
二等辺三角形の作図は、三角形が無いし、交点の判断以外は難しくないので、飛ばすことにしよう。
じゃあ、クラスタの貼り合わせ。しかしそうすると、cluster_lstも必要なんじゃないか。凄い量だけど、新しい3つの情報は全てセットのようなものだから、自分な中では自然に思える。
試しにADで反転させるなら、元BをE、元CをFとして、
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]]
[[A, E, F, D], [DAE_p, AE, AEF_p, EF, DFE_p, DF, ADF_p, AD]]
というようなイメージなんだが、まずgraphにこのクラスタの通りにEとFと辺を追加する。
いやしかし、点Aに新しく追加したAEだけど、AD上の点だとか、AB上の点と繋がってないわけで、あの方法が使えないのか。
新しく作った角BAEとかがプラスにならなくても、貼り合わせるということだけはやる予定なんだが。
今まではgraphを更新し、cluster_lstに対応するように登録して、後はイコールだとかを登録する流れだった。作った角の和がポジティブだったら、合体させてそれもcluster_lstに登録していた。
今回は、それに加えて、angle_lstやclockwise_lstやcoplanar_lstも登録する必要がある。angle_lstは角の和がポジティブだと分からない状態では、バラバラに登録するしか無い。clockwise_lstは今回は難しくないと思うけど、どちらもポジティブだし。coplanar_lstも難しくないし。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[F], [], []]
]
,
E : [
[[A], [], []],
[[F], [], []]
]
,
F : [
[[D], [], []],
[[E], [], []]
]
];
clockwise_lst := [
A : [
[B, [], [], [D, E]],
[D, [B], [], [E]],
[E, [B, D], [], []]
~
]
,
B : [
[C, [], [], [A]],
[A, [C], [], []],
~
]
,
C : [
[D, [], [], [B]],
[B, [D], [], []],
~
]
,
D : [
[A, [], [], [C, F]],
[C, [A], [], [F]],
[F, [A, C], [], []]
~
]
,
E : [
[A, [F], [], []],
[F, [], [], [A]],
~
]
,
F : [
[E, [D], [], []],
[D, [], [], [E]],
~
]
];
angle_lst := [
A : [
[
[B, [], [], [D]],
[D, [B], [], []]
]
,
[
[D, [], [], [E]],
[E, [D], [], []]
]
]
,
B : [
[
[C, [], [], [A]],
[A, [C], [], []]
]
]
,
C : [
[
[D, [], [], [B]],
[B, [D], [], []]
]
]
,
D : [
[
[A, [], [], [C]],
[C, [A], [], []]
]
,
[
[F, [], [], [D]],
[D, [F], [], []]
]
]
,
E : [
[
[A, [F], [], []],
[F, [], [], [A]]
]
]
,
F : [
[
[E, [D], [], []],
[D, [], [], [E]]
]
]
];
parallel_lines_lst := [
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, E, F, D], [DAE_p, AE, AEF_p, EF, DFE_p, DF, ADF_p, AD]]
];
always {
ABC_p == 168;
BCD_p == 108;
AB == BC == CD;
AEF_p == 168;
DFE_p == 108;
AE == EF == DF;
後はクラスターの対応する部分をイコールで
}
こういうイメージだ。適当だったけど。
クラスターの角を、時計回りを基準に反転させるのがちょっと違う作業だったのかな。
この後の作業は無視しているし、(条件が判明し次第の角の)統合とかの作業もあるはずなのだけど。
一晩開けて思うのだけど、自動化を視野に入れたかったから書かなかったけど、イコールで無く以上以下を視野に入れれば、この角の和はポジティブだと分かるし、だからクラスタとしても登録できる。angle_lstにも登録できる。
同一平面上にあって、クラスタが同じ辺を共有していて、その角の和が両方180°以下の時に、新しいクラスタとして登録する、というのは毎回作図後のフェーズで確認しよう。
angle_lstもclockwise_lstから同じように毎回拡張できるようにしたいが。あるいはangle_lst同士か?本当に模索中なんで。
いや、angle_lst同士だろうな。時計回りだから可能になる。同じ点を共有していて、途中とでも足し合わせたらプラスになるなら、大きくできるか、新しく追加できるか、どちらかはまだ分からないが。
角の呼び方を時計回りに限定する、っていうのもアリなんだよな。そうすると、少なくとも角1や角2よりは明解になる。
それは良い考えだと思うしぜひ採用したいが、その時には角が180°以下だとどういうルートで判断するかが問題になるだろうな。
次の正三角形も、交点の判定の仕方はもう考えたし、角の割り方も位置関係が分からないなら分からないなりに方法を用意してあるし、考えなくても良いんじゃないかな。
とりあえず、他の問題でもこの方法論が通用するか見ていこう。それであと可能だと分かったらポジティブやネガティブを撤廃しよう。プログラムは、全てのジャンルで通用するかを調べていって、作るにしても最後に作れば良いんじゃないかな。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その25
ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。交点の確認はこの方法を使う。
06年度トライアル問題 問題9
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
 』
』
では初期条件。
graph := [
A : [
[[B], []],
[[D], []]
]
,
B : [
[[A], []],
[[C], []]
]
,
C : [
[[B], []],
[[D], []]
]
,
D : [
[[A], []],
[[C], []]
]
];
parallel_lines_lst := [
];
triangle_lst := [
];
always {
ABC_p == 168;
BCD_p == 108;
AB == BC == CD;
}
辺による辺の和も180°の角の和も無し。平行線も無し。graphを辿っても三角形は見つからない。前回説明した方法での角の和の登録も、使う必要無し。
作図
セットアップが終わったので、作図に移る。
セットアップ時の角の和の取得法について - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その21 - ニート歴10年からの数学日記の後半、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その18 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その17 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その16 - ニート歴10年からの数学日記、
辺りを参考にしようかな、後ろに行くほどもう参考にならないと思うけど。
- ?正四角形の判定
- ?正五角形の判定
まず点と点を結ぶ所から。
graphの最初のAを確認して、graphの繋がっていないCと単純に繋げる。
graph := [
A : [
[[B], []],
[[D], []],
[[C], []]
]
,
B : [
[[A], []],
[[C], []]
]
,
C : [
[[B], []],
[[D], []],
[[A], []]
]
,
D : [
[[A], []],
[[C], []]
]
];
交点を判断するのに三角関数を使うなら、実はこの段階でもう答えは分かってしまう。ACの(CDと比べた時の)長さは分かるし、角ACDも分かるし、それで角ADCも分かってしまう(いや、ACDはBCDの角の和が分からないと計算できないか)。
まあ流れとしては、セットアップ時の角の和の取得法について - ニート歴10年からの数学日記の後半で書いたようなことを、順番なんか適当で、乱れ打ちでやってしまう。
交点の発見は、作図されたACに繋がっている辺と辺で、片っ端から三角関数にかけていく。更にはACに繋がった辺を基準に、ACと他の辺で三角関数にかけていく。
おそらくそういう風になるだろう。
交点が発生したら、その交点について最初にやるみたいに、辺の和だとかを登録していく。
更に、角だとか辺の大きさが明らかになるたびに、その角や辺について同じように片っ端から三角関数にかけていく。今は計算量のことは何も考えていない。
なんかそれぐらいのラフさでゴールまで行ける気がする。作図後の角の和については、まだ問題があるが。
最適化については、この程度の計算量なら、動いた後に考えれば良い。
もしクラスタがあれば、AとCを繋げた時に、角の和を登録できるんだがな。このままでは、Bを基準に考えたとしても、例えばDが今とは反対側にあるという場合もあり得るんじゃないか。辺と辺の繋がりでは無く、中の面で捉える必要があるのではないか。そうでなければ角の和は登録できないのではないか。
ちょっと今日は寝不足なのか、調子が悪い。
よく考えたら、三角関数は、辺がZのように繋がっている時はどうなるのだろう。点と点の間でも、辺の並びは時計回りとかで統一した方が良いのだろうか。ある辺から、左回りと右回りでポジティブな角同士の時だけに、三角関数を適用すべきなのだろうか。
それならできるような気もするが、分からん。
どうなんだろうと思ったが、平行線リストの亜種みたいなものなのかもしれない。3点が平面上にあって、1辺を基準にした2種類の最大のポジティブの角で、時計回りと反時計周りだったら、三角関数の対象になる。
交点を判定して、その後に発生する角の和も180°の角の和なんで簡単なんで良いとして、問題は点に辺を付け加える時の角の和の更新だろう。
その付け加える辺がAB、元々あった辺をACとして、辺AB上の点がACと繋がっていたら、時計回りとかを利用すれば2辺の位置関係は分かるのではないか。
例えば、普通にAとBがCと繋がっているとして、Cが左にあったらCにおいてA, Bの順番だし、Cが右にあったらB, Aだ。
2辺の関係が分かれば、何と何の間なのかは分かるだろう。他に方法ってあるのかな。
ただ、辺において点の位置が不確定なことがあったように、点においても辺と辺の位置が不確定なことがあるはずで、それに対応することを考えると面倒くさい。
二つの形式を考えた。
C : [
F : [[], [], [B, H, G, D]],
B : [[F], [], [H, G, D]],
H : [[F, B], [], [G, D]],
G : [[F, B, H], [], [D]],
D : [[F, B, H, G], [], []]
]
C : [
[[], F, [], [B, H, G, D]],
[[F], B, [], [H, G, D]],
[[F, B], H, [], [G, D]],
[[F, B, H], G, [], [D]],
[[F, B, H, G], D, [], []]
]まあどっちでも良いんだけども。こういうの、必要なんじゃないのかな。
自分で書くのが面倒くさい場合は、内部でテキストというか形式を生成して使っても良いかもしれない。そういう風に考えれば良いんじゃないのかな。
作図自体は問題にはならないだろう、多分(いや、作図の時に角の和だけは割っておく必要があるのかな?)。今日はここで終わりにしておく。
セットアップ時の角の和の取得法について
人間が認識できる解答に必要な情報を完全に取得するということを考えた時に、クラスタによる取得は不完全だと言わざるを得ないのではないかと思う。
例えば、1つの点から複数の辺が伸びていて、それらのもう一方の端を全て輪のように繋げた図を想像してみる。すると、この時に角の和は一切取得できない。外側のクラスタから見て、真ん中の辺は折れ曲がっていて、素直にクラスタを割った状態になっていないからだ。しかし、人間は角の和を見て取得することができてしまうわけだ。
人間は、平面における辺の並びを見ることができてしまう、また、ポジティブかネガティブかも見ることができてしまう。
やっぱり角の和が曲者で、他は全て自然な取得法になっているのではないかと思う。辺による辺の和と180°の角の和を取得して、平行線(同じ方向の辺)同士による角のイコールを取得して、三角形による色々を取得する、全く合理的であると思う。
なぜ角の和が難しいのかを考えると、辺が反対方向に突き抜けるようになっているからというか、360°で一周するからなのだと思う。もし180°であれば、端と端を登録して、例えば点Aに対して点B、C、D、Eの順番で繋がっているとしたら、[A, [B, C, D, E]]のように登録すれば、角の和を効率的に(また人間がやるように)取得することができる。しかし180°以上のが一つでも交じると、その後側でポジティブな角の和が発生するかもしれず、一気にややこしくなる。
二種類の方法を考えた。
まず一つ目は、さっき書いたような取得法をそのまま使うことで、180°以上のがあるなら、一つの点に対して複数回同じ方法を使う、という方法。
もう一つは、そもそも問題文の角のポジティブやネガティブは最初から不完全な情報であり、人間としても取得しないという方法で、挟んだ辺と一緒に角1や角2という風に名付け、180°以上だと判明し次第ポジティブやネガティブと名付け直す、あるいはそもそも名付け直さない、という方法。
どちらの方法が良いかは分からないのだけど、とりあえず平和的に最初の方を採用することにする。それでまあ問題文の図から角の和を取得することはできるわけだ。
作図をする段階で、なにか新しい角の和の取得方法や解釈が出てくるかもしれない。
クラスタについて考えるのは全く無駄では無かったと思うけど、とりあえず人間が認識できる解答に必要な情報を完全に取得するという観点で、そういうことにした。
これは追記になるのだが、角1や角2と名付ける場合は、まずそれぞれの点において、繋がっている点を循環リストにして、挟まっている点と一緒に機械的に登録していく。その時に挟まっている点が少ない方を角1としても良いし、全く適当でも良い。
で、前者のポジティブかネガティブか判別する方なのだけど、これは点と繋がっている点ごとに、2種類の最大のポジティブが登録できるわけだが、この情報は見方を反転させれば最小のネガティブでもある。その情報を使えば、ネガティブとポジティブでネガティブになる角の和を登録することもできるし、ポジティブとポジティブでネガティブになる角の和を登録することもできる。
いや、ただ、ポジティブとポジティブでネガティブになる角の和の場合、ネガティブな方が最小じゃない場合が漏れてしまうのか?そこはもう少し、凝った仕組みにする必要があるのか…。最小のネガティブな角の和に更に角を追加したものが、ポジティブな角とポジティブな角に分割できるか。
更に追記になるのだが、作図と交点などの確認は考え方としては分けた方が良いかもしれない。作図は定義通りにシンプルに済ませて、確認の方を手間をかけるというかループさせる。
やることと言えば、まず交点を発見する。でもし発見したら、その交点について、辺の和や180°の角の和を登録、平行線で角のイコールを登録、三角形が新しくできてないか探す、三角形定理ループを回す、と最初のセットアップのような動きをする。
違う所と言えば、角の和の発見で、今回のが通用すれば今回のを使うし、通用しなければクラスタを使うことになるかもしれない(クラスタの発見や、クラスタの分割など)。
あとは、不確定なものの確定もする必要がある。具体的には角1や2がネガティブかポジティブか、辺において順番が不確定なものを制約でできるだけ確定させる、などの作業をする必要がある。
(よく分からないけど、それぐらいかな。必要なものがあれば試行錯誤している内に出てくると思うけど。)
3つのステップで一つでも明らかになったら、三角形定理ループみたいにループして、どのステップでも何も明らかにならない状態を目指す。三角形定理ループも別に分けて4ステップにした方が良いかな?
二次元上のユークリッド幾何の問題 その24
ジュニア算数オリンピック・算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。作業手順は今はこれを参考にする。
算数オリンピック13年度トライアル問題 問題10
『図の四角形ABCDで、点E、F、G、H、MはAE : EB = AF : FD = 2 : 5、BG : GH : HC = 3 : 2 : 2、CM = DMを満たす辺上の点です。いま、EG、FH上にそれぞれEP = PG、FQ = QHとなる点P、Qをとるとき、PQ = BMを求めなさい。
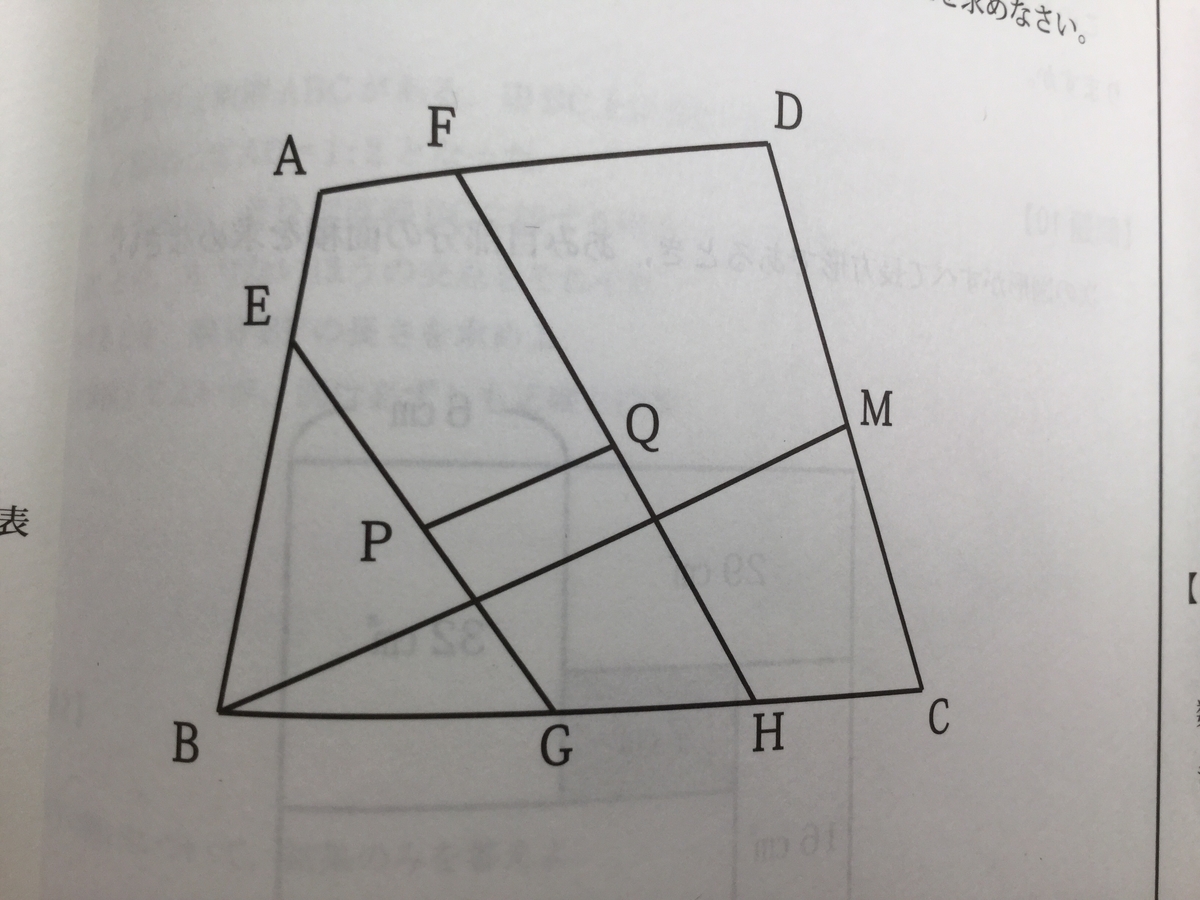 』
』
昨日の続きで、今日はクラスタに直線の点も入れて同じ作業をする。
名付けられていない交点は、上からR、Sと名付ける。今回は、最初から全体をクラスタとして登録する。
graph := [
A : [
[[F, D], []],
[[E, B], []]
]
,
B : [
[[E, A], []],
[[S, R, M], []],
[[G, H, C], []]
]
,
C : [
[[B, G, H], []],
[[D, M], []]
]
,
D : [
[[A, F], []],
[[M, C], []]
]
,
E : [
[[A], [B]],
[[P, S, G], []]
]
,
F : [
[[A], [D]],
[[Q, R, H], []]
]
,
G : [
[[B], [H, C]],
[[E, P, S], []]
]
,
H : [
[[B, G], [C]],
[[F, Q, R], []]
]
,
M : [
[[D], [C]],
[[B, S, R], []]
]
,
P : [
[[E], [S, G]],
[[Q], []]
]
,
Q : [
[[P], []],
[[F], [R, H]]
]
,
R : [
[[F, Q], [H]],
[[B, S], [M]]
]
,
S : [
[[E, P], [G]],
[[B], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
}今回はここからスタート。
で、graphを見て、辺の和と、180度の角の和を登録する。
平行線リストを見て、平行線による角のイコールも登録する。
三角形も登録する。graphを見て、点と繋がっている点と点が繋がっていたら、三角形。
graph := [
A : [
[[F, D], []],
[[E, B], []]
]
,
B : [
[[E, A], []],
[[S, R, M], []],
[[G, H, C], []]
]
,
C : [
[[B, G, H], []],
[[D, M], []]
]
,
D : [
[[A, F], []],
[[M, C], []]
]
,
E : [
[[A], [B]],
[[P, S, G], []]
]
,
F : [
[[A], [D]],
[[Q, R, H], []]
]
,
G : [
[[B], [H, C]],
[[E, P, S], []]
]
,
H : [
[[B, G], [C]],
[[F, Q, R], []]
]
,
M : [
[[D], [C]],
[[B, S, R], []]
]
,
P : [
[[E], [S, G]],
[[Q], []]
]
,
Q : [
[[P], []],
[[F], [R, H]]
]
,
R : [
[[F, Q], [H]],
[[B, S], [M]]
]
,
S : [
[[E, P], [G]],
[[B], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}
昨日と同じように、クラスタからクラスタを弾き出す。思考過程を晒す。今回は点だけに着目して、graphでクラスタ内でクラスタ以外の方法で繋がっているものを探していった。
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
BM
EG
FH
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
BM
[[B, G, H, C, M], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, BM]
[[A, E, B, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BM, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
EG
[[A, E, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EG, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, EG]]
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
FH
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FH]]
[[A, E, B, G, H, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, FH, AFQ_p AF]]
いや、本当は、交点の判定を先にするべきなのだろうな。
[A, E, B, G, H, C, M, D, F]
BM
EG
FH
[E, B, G, H, M, F]
BMには、B側にEG、M側にFH
EGとFHにBMと一つずつ
B : [
[[S, R, M], ],
]
M : [
[[B, S, R], ]
]
R : [
[[B, S], [M]]
]
S : [
[[B], [R, M]]
]
E : [
[[P, S, G], ]
]
G : [
[[E, P, S], ]
]
S : [
[[E, P], [G]],
]
F : [
[[Q, R, H], ]
]
H : [
[[F, Q, R], ]
]
R : [
[[F, Q], [H]],
]
PとS、QとRの位置関係はどう考えよう。
分からないのではないか?そうすると、どうしよう。
前者のPとSのケースについて考えてみる。
E : [
[[P, S, G], ]
]
G : [
[[E, P, S], ]
]
S : [
[[E, P], [G]],
]
P : [
[[E], [S, G]],
]
んー、こう考えてみるか?
E : [
[[P, S, G], ]
]
G : [
[[E, P, S], ]
]
S : [
[[E], [G]],
]
P : [
[[E], [G]],
]
修正前だと、E→P→S→G、あるいはG→S→P→Eが可能。修正後だと、E→S→、の後がGにおいてはE・P・Sなので続かない。そういう場合は無視すべきか?
あるいは、
E : [
[[P, S, G], , ]
]
G : [
[[E, P, S], , ]
]
S : [
[[E], [P], [G]],
]
P : [
[[E], [S], [G]],
]
一方から見て位置関係がどちらか分からないということは、もう一方からも分からないということではないか。
いやどうだろう、これは昔考えた「位置の制約」に近いのではないか。
EG ~ @{E < G, P, S}
EG ~ @{E, P, S < G}
EG ~ @{E < P < G}
EG ~ @{E < S < G}
だっけか?忘れたけど。
そういうものが確定しないと交点を認めないというスタンスでは、この問題のクラスタを取得し切ることはできない。1番目と2番目と3番目(位置の制約)について、2番目と3番目は本質的に同じだとして、1番目を試して駄目だったら、2番目を試すことにしよう。というか3番目は、できればこれ以上話をややこしくしたくない。
まあでもこれは、初期段階ならこの判断はいらないし、作図段階なら、更に少し作図して三角関数で素直に判定した方が良いのかもしれない。分からないなら本当にどちらか分からない状態なわけで、そんな状態でそういう機能で交点を考えるのに何の旨味があるのかというか。
一晩開けて思うのだけど、1番目と2番目は、大は小を兼ねるというか、2番目の真ん中を消せば1番目になるから、とりあえず2番目にしてみようかな。
そもそも交点を作らないというのが元々だったんだけど、そうするとクラスタEAFRSを考えることができなくなる。そういう順番が関わるみたいなのは、できれば避けたい。失敗し次第、その交点を作らない方針に戻すとして、だからとりあえず2番目で行こう。
まあ、今回は、そもそも作図で無く初期のセットアップだから、やり直さずこのまま続けるが。
BMの間は、B、S、R、M。BS, BSR_h, RS, BRM_h, MR。
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]]
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
EGの間は、E、P、S、G。EP, EPS_h, PS, ESG_h, GS。
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]]
FHの間は、F、Q、R、H。FQ, FQR_h, QR, FRH_h, HR
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]]
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}
いろいろ考察したんで、一旦表示した。続きをする。
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]]
GS
HR
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]]
GS
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]]
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]]
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]]
HR
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]]
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]]
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
ES
FR
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
ES
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, ES, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, ES]]
ES。E, P, S。EP, EPS_h, PS
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]]
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]]
FR
[[A, E, B, S, R, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, FR, AFQ_p, AF]]
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FR]]
FR。F、Q、R。FQ, FQR_h, QR。
[[A, E, B, S, R, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]]
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
MS
FH
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
MS
[[A, E, P, S, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, MS, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[S, G, H, C, M], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MS]],
MS。M、R、S。MR, BRM_h, RS
[[A, E, P, S, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[S, G, H, C, M], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
FH
[[A, E, P, S, G, H, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, FH, AFQ_p, AF]],
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FH]],
FH。F、Q、R、H。FQ, FQR_h, QR, FRH_h, HR。
[[A, E, P, S, G, H, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]]
BS
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]]
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]]
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
MR
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[M, D, F, Q, R], [BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRM_p, MR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
EG
BR
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
EG
[[A, E, G, H, R, Q, F], [EAF_p, AE, AEP_p, EG, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]]
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, EG]]
EG。E, P, S, G。EP, EPS_h, PS, ESG_h, GS。
[[A, E, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]]
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]]
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]]
BR
[[A, E, B, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BR, BRF_p, QR, FQR_h, FQ, AFQ_p AF]]
[[B, G, H, R], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, BR]]
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]],
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[A, E, B, S, R, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[S, G, H, C, M], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS]],
[[A, E, P, S, G, H, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[M, D, F, Q, R], [BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRM_p, MR]],
[[A, E, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[A, E, B, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BR, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, H, R], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, BR]]
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}
えー、続き。該当するものだけ表示することにする。
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
HR
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BHR_p, RS, GSR_p, GS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
FR
[[A, E, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, FR, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FR],
FR。F, Q, R。FQ, FQR_p, QR
[[A, E, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_p, FQ, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_p, QR],
[[A, E, B, S, R, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
ES
[[A, E, S, R, F], [EAF_p, AE, AEP_p, ES, ESR_p, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, ES]],
ES。E, P, S。EP, EPS_p, PS
[[A, E, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_p, PS, ESR_p, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_p, EP]],
[[A, E, P, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
FR
[[A, E, P, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, FR, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFR_p, FR]],
FR。FQ, FQR_p, QR
[[A, E, P, S, R, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_p, FQ, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFR_p, FQ, FQR_p, QR]],
[[S, G, H, C, M, R], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS]],
HR
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
RS
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
RS
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
MR
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[M, D, F, Q, R], [BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRM_p, MR]],
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
RS
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
RS
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[A, E, B, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BR, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
↑、今回はこういうミスが多かった、ほとんど書かずに直したが。[A, E, B, G, H, R, Q, F]の時に、BRの間にSがある。それが抜けているという単純ミスだ。早く自動化してえ、できないんだっけか?
BR。B, S, R。BS, BSR_h, RS。
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
ES
[[A, E, S, R, Q, F], [EAF_p, AE, AEP_p, ES, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, ES]],
[[B, G, H, R], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, BR]]
同じくSが抜けている。ただしRBなので注意。
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, RS, BSR_h, BS]]
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, RS, BSR_h, BS]]
GS
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]]
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BRH_p, RS, GSR_p, GS]]
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]],
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, S], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[R, M, D, F], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[S, G, H, C, M], [GSR_p, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS]],
[[A, E, P, S, G, H, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[H, C, M, D, F], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[M, D, F, Q, R], [BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRM_p, MR]],
[[A, E, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[E, B, G], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[B, G, H, R], [GBS_p, BG, BGH_h, GH, BHF_p, HR, BRH_p, BR]]
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BHR_p, RS, GSR_p, GS]],
[[R, M, D, F, Q], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_p, QR],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}いろいろ消えた。被ってたんで。
では続き。
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
RS
[[P, S, R, Q], [QPS_p, PS, ESR_p, RS, BRF_p, QR, PQR_p, PQ]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
PQ
[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP, FQ, AFQ_p, AF]],
[P, S, R, Q], [QPS_p, PS, ESR_p, RS, BRF_p, QR, PQR_p, PQ]],
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]],
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, P, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[R, M, D, F, Q], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BHR_p, RS, GSR_p, GS]],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
[[P, S, R, Q], [QPS_p, PS, ESR_p, RS, BRF_p, QR, PQR_p, PQ]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP, FQ, AFQ_p, AF]],
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}目視で確認して、だいぶインチキというか削ったが、まあ単純ミスだろうし、良しとしよう。
って、角の和を登録するのを忘れていたか。
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]]
BM
とか、こういう段階で、クラスタのBかMの角がハーフで無くポジティブの時に、角の和を登録する。
今回はBがポジティブで、EBM(適当)とMBGが、足したらEBG_pになると登録する。
EBS_p + GBS_p == MBG_p、という具合。
他は無かった。いやあるんだが、まあそういうことだ。
graph := [
A : [
[[F, D], [], []],
[[E, B], [], []]
]
,
B : [
[[E, A], [], []],
[[S, R, M], [], []],
[[G, H, C], [], []]
]
,
C : [
[[B, G, H], [], []],
[[D, M], [], []]
]
,
D : [
[[A, F], [], []],
[[M, C], [], []]
]
,
E : [
[[A], [], [B]],
[[P, S, G], [], []]
]
,
F : [
[[A], [], [D]],
[[Q, R, H], [], []]
]
,
G : [
[[B], [], [H, C]],
[[E, P, S], [], []]
]
,
H : [
[[B, G], [], [C]],
[[F, Q, R], [], []]
]
,
M : [
[[D], [], [C]],
[[B, S, R], [], []]
]
,
P : [
[[E], [], [S, G]],
[[Q], [], []]
]
,
Q : [
[[P], [], []],
[[F], [], [R, H]]
]
,
R : [
[[F, Q], [], [H]],
[[B, S], [], [M]]
]
,
S : [
[[E, P], [], [G]],
[[B], [], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
[[A, E, B, G, H, C, M, D, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[B, G, H, C, M, R, S], [GBS_p, BG, BGH_h, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, BSR_h, BS]],
[[A, E, B, S, R, M, D, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[A, E, P, S, G, H, C, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHC_h, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, G, S, P], [BEP_p, BE, EBG_p, BG, BGE_p, GS, ESG_h, PS, EPS_h, EP]],
[[H, C, M, D, F, Q, R], [CHF_p, CH, BCD_p, CM, CMD_h, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR, FRH_h, HR]],
[[A, E, B, G, H, R, Q, F], [EAF_p, AE, AEB_h, BE, EBG_p, BG, BGH_h, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p AF]],
[[B, G, S], [GBS_p, BG, BGE_p, GS, BSG_p, BS]],
[[G, H, C, M, R, S], [EGH_p, GH, BHC_h, CH, BCD_p, CM, BMC_p, MR, BRM_h, RS, GSR_p, GS]],
[[B, G, H, R, S], [GBS_p, BG, BGH_h, GH, BHF_p, RH, BRH_p, RS, BSR_h, BS]],
[[H, C, M, R], [CHF_p, CH, BCD_p, CM, BMC_p, MR, HRM_p, HR]],
[[A, E, P, S, R, M, D, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRM_h, MR, BMD_p, DM, ADM_p, DF, AFD_h, AF]],
[[E, B, S, P], [BEP_p, BE, EBS_p, BS, BSE_p, PS, EPS_h, EP]],
[[A, E, B, S, R, Q, F], [EAF_p, AE, AEB_h, BE, EBS_p, BS, BSR_h, RS, BRF_p, QR, FQR_h, FR, AFQ_p, AF]],
[[R, M, D, F, Q], [FRM_p, MR, BMD_p, DM, ADM_p, DF, DFQ_p, FQ, FQR_h, QR]]
[[A, E, P, S, G, H, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, FQR_h, FQ, AFQ_p, AF]],
[[G, H, R, S], [EGH_p, GH, BHF_p, HR, BHR_p, RS, GSR_p, GS]],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP_p, FQ, AFQ_p, AF]],
[[P, S, G, H, R, Q], [QPS_p, PS, ESG_h, GS, EGH_p, GH, BHF_p, HR, FRH_h, QR, PQR_p, PQ]],
[[A, E, P, S, R, Q, F], [EAF_p, AE, AEP_p, EP, EPS_h, PS, ESR_p, RS, BRF_p, QR, FQR_h, FQ, AFQ_p, AF]],
[[P, S, R, Q], [QPS_p, PS, ESR_p, RS, BRF_p, QR, PQR_p, PQ]],
[[S, G, H, R], [GSR_p, GS, EGH_p, GH, BHF_p, HR, BRH_p, RS]],
[[A, E, P, Q, F], [EAF_p, AE, AEP_p, EP, EPQ_p, PQ, FQP, FQ, AFQ_p, AF]],
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h;
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
EBS_p + GBS_p == MBG_p;
}これでセットアップは終わりだろう。長かった。
いや、誤解を生みそうだけど、今回のは終わりってことね。おそらくまだ続く。
二次元上のユークリッド幾何の問題 その23
ジュニア算数オリンピック・算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。作業手順は今はこれを参考にする。
算数オリンピック13年度トライアル問題 問題10
『図の四角形ABCDで、点E、F、G、H、MはAE : EB = AF : FD = 2 : 5、BG : GH : HC = 3 : 2 : 2、CM = DMを満たす辺上の点です。いま、EG、FH上にそれぞれEP = PG、FQ = QHとなる点P、Qをとるとき、PQ = BMを求めなさい。
 』
』
名付けられていない交点は、上からR、Sと名付ける。
graph := [
A : [
[[F, D], []],
[[E, B], []]
]
,
B : [
[[E, A], []],
[[S, R, M], []],
[[G, H, C], []]
]
,
C : [
[[B, G, H], []],
[[D, M], []]
]
,
D : [
[[A, F], []],
[[M, C], []]
]
,
E : [
[[A], [B]],
[[P, S, G], []]
]
,
F : [
[[A], [D]],
[[Q, R, H], []]
]
,
G : [
[[B], [H, C]],
[[E, P, S], []]
]
,
H : [
[[B, G], [C]],
[[F, Q, R], []]
]
,
M : [
[[D], [C]],
[[B, S, R], []]
]
,
P : [
[[E], [S, G]],
[[Q], []]
]
,
Q : [
[[P], []],
[[F], [R, H]]
]
,
R : [
[[F, Q], [H]],
[[B, S], [M]]
]
,
S : [
[[E, P], [G]],
[[B], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
];
cluster_lst := [
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
}じゃあ、ここからスタート。クラスタは、前回と同じく最初は登録しない。
辺の和を登録する。
辺を区切ることによる180°の角の和も登録する。
平行線リストを見て、角のイコールも登録する。
三角形も登録する。graphの点と繋がっている点が更に別の繋がっている点と繋がっていたら、三角形。
辺を区切ることによる180°の角の和を登録することで、対頂角のイコールは自動的に弾き出されるし、三角形の外角も自動的に弾き出される。
graph := [
A : [
[[F, D], []],
[[E, B], []]
]
,
B : [
[[E, A], []],
[[S, R, M], []],
[[G, H, C], []]
]
,
C : [
[[B, G, H], []],
[[D, M], []]
]
,
D : [
[[A, F], []],
[[M, C], []]
]
,
E : [
[[A], [B]],
[[P, S, G], []]
]
,
F : [
[[A], [D]],
[[Q, R, H], []]
]
,
G : [
[[B], [H, C]],
[[E, P, S], []]
]
,
H : [
[[B, G], [C]],
[[F, Q, R], []]
]
,
M : [
[[D], [C]],
[[B, S, R], []]
]
,
P : [
[[E], [S, G]],
[[Q], []]
]
,
Q : [
[[P], []],
[[F], [R, H]]
]
,
R : [
[[F, Q], [H]],
[[B, S], [M]]
]
,
S : [
[[E, P], [G]],
[[B], [R, M]]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△BES : [EBS, BE, BEP, ES, BSE, BS],
△BEG : [EBS, BE, BEP, EG, BGE, BG],
△BGS : [GBS, BG, BGE, GS, BSE, BS],
△BHR : [GBS, BH, BHF, HR, BRH, BR],
△BCM : [GBS, BC, BCD, CM, BMC, BM]
];
cluster_lst := [
];
always {
BE * 2 == AE * 5;
DF * 2 == AF * 5;
BG * 2 == GH * 3;
BG * 2 == CH * 3;
GH == CH;
CM == DM;
EP == PG;
FQ == HQ;
AE + BE == AB;
AF + DF == AD;
BG + GH == BH;
BG + CG == BC;
BH + CH == BC;
GH + CH == CG;
DM + CM == CD;
EP + PS == ES;
EP + GP == EG;
FQ + QR == FR;
FQ + HQ == FH;
FR + HR == FH;
QR + HR == QH;
BR + MR == BM;
RS + MR == MS;
ES + GS == EG;
PS + GS == GP;
BS + RS == BR;
BS + MS == BM;
AEP_p + BEP_p == AEB_h; #180と登録した方が良かったかな
AFQ_p + DFQ_p == AFD_h;
BGE_p + EGH_p == BGH_h;
BHF_p + CHF_p == BHC_h;
BMD_p + BMC_p == CMD_h;
EPQ_p + QPS_p == EPS_h;
FQP_p + PQR_p == FQR_h;
BRF_p + BRH_p == FRH_h;
FRM_p + HRM_p == FRH_h;
BRF_p + FRM_p == BRM_h;
BRH_p + HRM_p == BRM_h;
BSE_p + BSG_p == ESG_h;
ESR_p + GSR_p == ESG_h;
BSE_p + ESR_p == BSR_h;
BSG_p + GSR_p == BSR_h;
}で、ここで気付いたけど、この後どうやっても、この三角形BCEとBCMの外でクラスタが登録されることは無い。だから、ABCDをクラスタとして登録してみることにした。
前回と同じく、作業手順を示す、大雑把な思考過程というか。クラスタの点を更新したら、基本的に角や辺は考え直している。
[[A, B, C, D], [EAF, AB, EBG, BC, BCD, CD, ADM, AD]]
AE + BE == AB; E EG
AF + DF == AD; F FH
BG + CG == BC; G
BH + CH == BC; H
DM + CM == CD; M BM
[[A, B, C, D], [EAF, AB, EBG, BC, BCD, CD, ADM, AD]]
AE + BE == AB;
BG + CG == BC;
EG
[[A, E, G, C, D], [EAF, AE, AEP, EG, EGH, CG, BCD, CD, ADM, AD]]
[[E, B, G], [BEP, BE, EBG, BG, BGE, EG]]
[[A, B, C, D], [EAF, AB, EBG, BC, BCD, CD, ADM, AD]]
AF + DF == AD;
BH + CH == BC;
FH
[[A, B, H, F], [EAF, AB, EBG, BH, BHF, FH, AFQ, AF]]
[[F, H, C, D], [DFQ, FH, BHF, CH, BCD, CD, ADM, DF]]
[[A, B, C, D], [EAF, AB, EBG, BC, BCD, CD, ADM, AD]]
DM + CM == CD;
BM
[[A, B, M, D], [EAF, AB, EBS, BM, BMD, DM, ADM, AD]]
[[B, M, C], [GBS, BM, BMC, CM, BCD, BC]] #手順において混乱がある
で、交点を考えなければいけないわけだが、一晩考えたんだが、三角関数を導入することにする。
でその前に、三角形の三辺が同じであれば合同は、俺はあの自分の考え方でも良いような気もしているが、しかし確かに厳密では無いかもしれない。
その場合は、まず角の二等分線の作図から、二等辺三角形の二辺が同じであればその底の方の二角も同じを証明する。まあ、二等分線を作図して、同じ長さの1辺とその共有する1辺とその間の角が同じだから合同をやる。
で、底辺から同じ長さの2辺が伸びているが角度は違うものを仮定して、その2つの三角形の頂点を結ぶ。そうすると二つの二等辺三角形ができるが、それぞれの角がイコールなはずなのに、片方はもう一方に含まれるのに、もう片方はもう一方を含むということになって、矛盾するので2辺が同じであれば角度も同じということになる。
で、平行四辺形の底辺が同じであれば上の方は平行移動しても面積は同じの証明をして、そこから有名なピタゴラスの定理の証明をすれば良いだろう。
角度による辺の長さの割合の計算は、厳密にはどうすれば良いかは分からないが、とにかく三角形が定まれば辺や角の大きさを出すような、データやちょっとした対応付けを、ここでは三角関数と呼ぶことにしよう(wikipediaを見てみたら、この呼び名で合っているようだ)。
で、平面という概念を導入するかだが、前に言った、平面において1点から伸びる3辺があって、2辺のポジティブな角が、他2つの組み合わせのポジティブ角以上であれば、それがその2つの角の和になるみたいなことは、よく考えたらそんなことは無かった。大体角の大きさが同じな3辺を想像すれば良い。
だから、平面という概念を想定する利点があるとしたら、今の所は三角関数が成立するということだけだ。クラスタの外側から作図する時に、必要になる気もするが。
後は、クラスタについても少し考えた。ネガティブな角を含むクラスタの話だけど、よく考えたら2つの辺が繋がっている時に、ポジティブな角で繋がっているのかネガティブな角で繋がっているのかは分からない、というかどちらでもある。だからクラスタとは、辺の繋がりでは無く、その内側の面のことで、だから三角形を基礎に考えるのは正しいし、また面として確保されてなければならないという意味で、ネガティブな角を含むクラスタを考えるのは良くないんじゃないかと思う。
クラスタの交点に戻る。
クラスタな。[A, B, C, D]では無く、[A, E, B, G, H, C, M, D, F]と考えることができれば、交点ができるかだけなら判断は簡単なんだけどな。
例えば、EGとFHとBMの場合、EGとFHは循環リストで考えても、お互いに跨っていない。別にあるか、あるいは完全に覆っているか。こういう場合は交点はできない。
EGとBMなんかは分かりやすくて、循環リストで考えても、お互いに跨っている。こういう場合は交点ができる。
EGとBM、FHとBMで交点ができるとして、BMにできたその二つの交点の位置関係はどうやって考えれば良いだろうか。こういう2点それぞれの位置関係が分かれば、全てにおいて位置関係が分かるはずだと思うが、表記的にも。
[A, E, B, G, H, C, M, D, F]を、[B, G, H, C, M, D, F, A, E]と循環させてみて思うに、EGとFHのどちらかがどちらかを覆わないように配置して、それぞれが含んでいるBかMの方に点ができる、という考え方はどうだろうか。
問題は、例えばEGとFHも互い違いになっている場合だろう。
3辺のそれぞれ2点を、X、Y、Zで考えてみる。[X, Y, X, Y]が互い違いになっている状態、循環しても意味は変わらない。ここにXを2つ入れてみる。[X, Z, Y, Z, X, Y]と入れても、[X, Z, Y, X, Z, Y]と入れても、いや、前者は1つと3つを挟むパターンであり、後者は2つと2つを挟むパターンと言えるだろう。この2通りについて考えてみる。
まず[X, Z, Y, Z, X, Y]のパターン。手元で描いてみて分かったが、このパターンは[Z, Y, Z, X, Y, X]であって、Yの挟んだ側にZとの交点ができて、YのXとの交点はXが挟んだ側にできる。
次に[X, Z, Y, X, Z, Y]のパターン。これが内側に三角形ができるパターンで、厄介なんだよな。抽象化するなら円の内側に3本の辺という感じだけど。Zの辺があるとして、その一方から、三角形を作るとして隣り合う2つの辺でどちらが短くて済むか、三角関数で調べるしか無いんじゃないかなあ。X、Y、Zのそれぞれの2点の端の6通りで試して、どれか一つでも明らかになれば、位置関係はハッキリするんだが。よく考えたら、角を挟む場合が厄介なんだよな、三角形が作れないから。
ああ、あるいは、区切られた1本の辺の対でどちらが短いか、か?
まあ今回は前者であって、[A, E, B, G, H, C, M, D, F]はEG・FH・BMでは[E, B, G, H, M, F]なので、BMのB側にEGと交点ができて、M側にFHと交点ができるわけだ。って、今回は作図じゃないから、もうできてるのか。
クラスタは、これからは間の点も全部含むことにしよう。そっちの方が分かりやすいから。じゃあ今日は、もうこれで良いかな。
ジュニア算数オリンピック・算数オリンピックの幾何学系の問題リスト
問題数が足りないので、対象を算数オリンピックまで拡大した。ついでにジュニア算数オリンピックのメモもデジタル化した。
研究過程を晒すという意味もあって(記事数のノルマのためというのもあるけど)、記事にしておく。
「ジュニア算数オリンピックの問題の分類」
・2次元ユークリッド幾何学
02ファ7
03ファ2
04ファ6
06トラ9
07トラ5
08トラ12
09トラ10
12ファ7
13トラ4
・ユークリッド幾何学の面積
97トラ2 格子
97ファ2
98トラ5 円?
98ファ4 円?
99トラ4 格子
99トラ7 ?
99トラ8 どうしよう
99トラ14 種類が違う?例の
99ファ5 格子なのかなあ
00トラ4 格子
00トラ9
01トラ1 種類が違う?例の
01トラ2
01ファ5
02トラ4 種類が違う?例の
02トラ9 どっちかと言うと方程式
03ファ4
04トラ5
04ファ2
05トラ8
05ファ6 格子、なのか?やってみないと
06トラ7
06ファ7
07トラ2
07ファ6 cmだが面積では無い?
08トラ5
08ファ7
09ファ4
09ファ7
10トラ1 種類が違う?例の新しい種類では
10トラ7
10ファ4
11トラ9
11ファ4
12トラ10
13トラ10
13ファ2 cmだが面積では無い?
13ファ5
・3次元ユークリッド幾何学
97トラ5
97ファ5
03ファ7
09トラ11
12ファ4
・ユークリッド折る
97トラ7
98ファ7
02トラ9
03トラ2
03トラ4
03トラ15
・その他
09トラ3 反転では無く、切って付ける 変則だが2次元ユークリッドかも
「算数オリンピックの問題の分類」
・2次元ユークリッド
93トラ8
93ファ4
?94トラ7 円
?94ファ4
95トラ8
95ファ6
?96ファ5 円
?98ファ6
03ファ2
04トラ9
04ファ3 円
05ファ1 円? 星座
06トラ11 交わらないクラスタ
07ファ3
09トラ6
12トラ10 ?新しい種類の作図
13トラ4
13トラ10 ?比率、2対の辺がイコールだったら平行四辺形
・2次元ユークリッド面積
92トラ5
92ファ5 円についての説明
93トラ7
94トラ9
95トラ5
96トラ8
97ファ2
98トラ7 円コロコロ
98ファ4
98ファ7 なんか、新しい
99トラ4
99トラ6
00トラ6
00ファ4
00ファ6
01トラ2
01トラ7
01ファ4
01ファ5
02ファ3
03トラ12
03ファ4
04トラ5
04ファ6
05ファ3
05ファ6
05ファ7
06トラ5
06ファ2
06ファ7
07トラ4
07トラ8
08トラ5
08ファ3
08ファ7
10トラ7
10トラ12
10ファ2
11トラ8
11トラ11
11ファ4
12ファ7
13ファ5
・3次元ユークリッド
92トラ6
94トラ4
94トラ10 面積
94ファ5 面積
?96トラ9
96ファ4 体積
96ファ6 体積
97トラ5
00ファ7
02トラ2 立体
02トラ9 体積
05トラ9
08トラ10
・ユークリッド折る
93ファ5
96トラ2
02トラ3 折ってる
02トラ10
・その他のグラフとか
92ファ4
93ファ6
95トラ1
95ファ1
95ファ3
00トラ4
01トラ8
02ファ1
04トラ2
04トラ7
07トラ7
08ファ2
12ファ3
・分類が分からん
93トラ9 分からん
93トラ10 トポロジー的な
94ファ1 93トラ9に似ている その他グラフとかな気も、でもどうやって実装しよう
96ファ1 村の距離
97トラ2 93トラ9に似ている しかし、2次元ユークリッドかなあ
98トラ10 似ているシリーズ
98ファ3 似ているシリーズ まあ面積なのかもしれないけど、まとめやすいように、後から戻せるし