ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その22
ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。作業手順は今はこれを参考にする。
07年度トライアル問題 問題5
『xの角度を求めなさい。
 』
』
交点には、上からアルファベット順で名前を付けていく。同じ高さにあるものは、左から右へ付けていく。
graph := [
A : [
[[C, E], []],
[[D, F, H], []],
[[G], []]
]
,
B : [
[[C, D, G], []],
[[E, H], []]
]
,
C : [
[[A], [E]],
[[B], [D, G]]
]
,
D : [
[[A], [F, H]],
[[B, C], [G]
]
,
E : [
[[B], [H]],
[[A, C], []],
[[G, F], []]
]
,
F : [
[[A, D], [H]],
[[E], [G]]
]
,
G : [
[[A], []],
[[B, C, D], []],
[[E, F], []],
[[H], []]
]
,
H : [
[[G], []],
[[A, D, F], []],
[[B, E], []]
]
];
parallel_lines_lst := [
];
triangle_lst := [
];
cluster_lst := [
];
always {
DAG_p == 20; #答えで確認した。紛らわしいが
CBE_p == 50;
BGE_p == 65;
EGH_p == 15;
AHB_p == 30;
}
クラスタをどう設定するかが問題なんだが、今回はそれを探るために、あえて最初はクラスタには何も登録しないことにした。
三角形をまず更新することにする。graphを確認して、keyのvalueの中身で更にgraphを確認し、その中にkeyのvalueの中身と同じものがあれば(ただしkeyと同一直線上のは抜かす)、それらは三角形だ。
更に角のイコールを確認する。平行線のリストには何も無し。対頂角はCとDとFにある。
辺のイコールは定義通り。
辺の和を確認する。graphを確認して、ある点を跨る辺がある時は、辺の和として更新する。
graph := [
A : [
[[C, E], []],
[[D, F, H], []],
[[G], []]
]
,
B : [
[[C, D, G], []],
[[E, H], []]
]
,
C : [
[[A], [E]],
[[B], [D, G]]
]
,
D : [
[[A], [F, H]],
[[B, C], [G]
]
,
E : [
[[B], [H]],
[[A, C], []],
[[G, F], []]
]
,
F : [
[[A, D], [H]],
[[E], [G]]
]
,
G : [
[[A], []],
[[B, C, D], []],
[[E, F], []],
[[H], []]
]
,
H : [
[[G], []],
[[A, D, F], []],
[[B, E], []]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△ACD : [CAD_p, AC, ACD_p, CD, ADB_p, AD],
△ACG : [CAG_p, AC, ACD_p, CG, AGB_p, AG],
△AEF : [CAD_p, AE, AEG_p, EF, AFG_p, AF],
△AEH : [CAD_p, AE, AEH_p, EH, AHB_p, AH],
△AEG : [CAG_p, AE, AEG_p, EG, AGE_p, AG],
△ADG : [DAG_p, AD, ADG_p, DG, AGB_p, AG],
△AFG : [DAG_p, AF, AFG_p, FG, AGE_p, AG],
△AGH : [DAG_p, AG, AGH_p, GH, AHG_p, AH],
△BCE : [CBE_p, BC, BCE_p, CE, AEB_p, BE],
△BDH : [CBE_p, BD, BDF_p, DH, AHB_p, BH],
△BEG : [CBE_p, BE, BEG_p, EG, BGE_p, BG],
△BGH : [CBE_p, BG, BGH_p, GH, BHG_p, BH],
△CEG : [DCE_p, CE, AEG_p, EG, BGE_p, CG], #ミスで抜かしていた
△DFG : [FDG_p, DF, AFG_p, FG, BGE_p, DG],
△DGH : [FDG_p, DG, BGH_p, GH, AHG_p, DH],
△EGH : [GEH_p, EG, EGH_p, GH, BHG_p, EH],
△EFH : [GEH_p, EF, EFH_p, FH, AHB_p, EH],
△FGH : [GFH_p, FG, EGH_p, GH, AHB_p, FH]
];
cluster_lst := [
];
always {
DAG_p == 20; #答えで確認した。紛らわしいが
CBE_p == 50;
BGE_p == 65;
EGH_p == 15;
AHB_p == 30;
ACG_p == DCE_p;
ACD_p == BCE_p;
ADB_p == FDG_p;
ADG_p == BDF_p;
AFE_p == GFH_p;
AFG_p == EFH_p;
AC + CE == AE;
BC + CD == BD;
BC + CG == BG;
AD + DF == AF;
AD + DH == AH;
BD + DG == BG;
CD + DG == CG;
BE + EH == BH;
AF + FH == AH;
DF + FH == DH;
EF + FG == EG;
}
三角形からクラスタを登録する。
更に、クラスタの辺が、辺の和の全体になっていて、例えばその間の点と三角形のクラスタの頂点が結び付いていたら、その点も含めてクラスタとして登録できるし、角の和として登録できる。間の点と点が結び付いていたら、それでもクラスタの分割になって、クラスタとして登録できる。
新しい作業なので、過程を貼る。一番上が三角形で、その後は何となく察してほしい。
ACG
CD + DG == CG;
AD
[[A, C, D, G], [CAG_p, AC, ACD_p, CD, CDG_h, DG, AGB_p, AG]],
CAD_p + DAG_p == CAG_p;
AEF
AC + CE == AE;
AD + DF == AF;
CD
[[C, E, F, D], [DCE_p, CE, AEG_p, EF, AFG_p, DF, BDF_p, CD]]
AEH
AF + FH == AH;
EF
[A, E, H, F], [CAD_p, AE, AEH_p, EH, AHB_p, AF, AFH_h, FH]
AEG_p + GEH_p == AEH_p;
AEH
AC + CE == AE;
AD + DH == AH;
CD
[C, E, H, D], [DCE_p, CE, AEH_p, EH, AHB_p, DH, BDF_p, CD],
AEG
AC + CE == AE;
CG
[[A, C, E, G], [CAG_p, AC, ACD_h, CE, AEG_p, EG, AGE_p, AG]],
AGB_p + BGE_p == AGE_p;
AEG
EF + FG == EG;
AF
[[A, E, F, G], [CAG_p, AE, AEG_p, EF, EFG_h, FG, AGE_p, AG]],
CAD_p + DAG_p == CAG_p;
AFG
AD + DF == AF;
DG
[[A, D, F, G], [DAG_p, AD, ADF_h, DF, AFG_p, FG, AGE_p, AG]],
AGB_p + BGE_p == AGE_p;
AGH
AD + DH == AH;
DG
[[A, G, H, D], [DAG_p, AG, AGH_p, GH, AHG_p, DH, ADF_h, AD]],
AGB_p + BGH_p == AGH_p;
AGH
AF + FH == AH;
FG
[[A, G, H, F], [DAG_p, AG, AGH_p, GH, AHG_p, FH, AFH_h, AF]],
AGE_p + EGH_p == AGH_p;
BDH
BC + CD == BD;
BE + EH == BH;
CE
[[C, D, H, E], [DCE_p, CD, BDF_p, DH, AHB_p, EH, AEH_p, CE]],
BDH
BE + EH == BH;
DF + FH == DH;
EF
[[E, B, D, F], [BEG_p, BE, CBE_p, BD, BDF_p, DF, AFE_p, EF]],
BEG
BC + CG == BG;
CE
[[B, E, G, C], [CBE_p, BE, BEG_p, EG, BGE_p, CG, BCD_h, BC]],
BEA_p + AEG_p == BEG_p;
BEG
BD + DG == BG;
EF + FG == EG;
DF
[[B, E, F, D], [CBE_p, BE, BEG_p, EF, AFE_p, DF, BDF_p, BD]],
BGH
BD + DG == BG;
DH
[[B, D, G, H], [CBE_p, BD, BDG_h, DG, BGH_p, GH, BHG_p, BH]],
AHB_p + AHG_p == BHG_p;
BGH
BE + EH == BH;
EG
[[B, G, H, E], [CBE_p, BG, BGH_p, GH, BHG_p, EH, BEH_h, BE]],
BGE_p + EGH_p == BGH_p;
BGH
BE + EH == BH;
BC + CG == BG;
CE
[[C, G, H, E], [DCE_p, CG, BGH_p, GH, BHG_p, EH, AEH_p, CE]],
???
BGH
BC + CG == BG;
BD + DG == BG;
CD
[[B, G, H], [CBE_p, BG, BGH_p, GH, BHG_p, BH]],
???
CEG
CD + DG == CG;
EF + FG == EG;
DF
[[C, E, F, D], [DCE_p, CE, AEG_p, EF, AFE_p, DF, BDF_p, CD]],
DGH
DF + FH == DH;
FG
[[D, G, H, F], [FDG_p, DG, BGH_p, GH, AHG_p, FH, AFH_h, DF]],
BGE_p + EGH_p == BGH_p;
EGH
EF + FG == EG;
FH
[[E, F, G, H], [GEH_p, EF, EFG_h, FG, EGH_p, GH, BHG_p, EH]],
AHB_p + AHG_p == BHG_p;
更に、graphを確認して、辺によって辺の180°が区切られているようなのを探して登録する。対頂角は登録されているので、半分ほど省けるだろう。
三角形に着目して、外角も登録する。いや、外角は登録しなくても良いな。三角形の内角は自動的に合計180°だと登録されるし、辺を辺で区切ることによる180°も登録されるので(そういう風にする)、自動的に弾き出される。(よく考えると、対頂角も自動的に取得されるか?)(錯角も自動的にと記述していたが、いや、でもそれも?)
graph := [
A : [
[[C, E], []],
[[D, F, H], []],
[[G], []]
]
,
B : [
[[C, D, G], []],
[[E, H], []]
]
,
C : [
[[A], [E]],
[[B], [D, G]]
]
,
D : [
[[A], [F, H]],
[[B, C], [G]
]
,
E : [
[[B], [H]],
[[A, C], []],
[[G, F], []]
]
,
F : [
[[A, D], [H]],
[[E], [G]]
]
,
G : [
[[A], []],
[[B, C, D], []],
[[E, F], []],
[[H], []]
]
,
H : [
[[G], []],
[[A, D, F], []],
[[B, E], []]
]
];
parallel_lines_lst := [
];
triangle_lst := [
△ACD : [CAD_p, AC, ACD_p, CD, ADB_p, AD],
△ACG : [CAG_p, AC, ACD_p, CG, AGB_p, AG],
△AEF : [CAD_p, AE, AEG_p, EF, AFG_p, AF],
△AEH : [CAD_p, AE, AEH_p, EH, AHB_p, AH],
△AEG : [CAG_p, AE, AEG_p, EG, AGE_p, AG],
△ADG : [DAG_p, AD, ADG_p, DG, AGB_p, AG],
△AFG : [DAG_p, AF, AFG_p, FG, AGE_p, AG],
△AGH : [DAG_p, AG, AGH_p, GH, AHG_p, AH],
△BCE : [CBE_p, BC, BCE_p, CE, AEB_p, BE],
△BDH : [CBE_p, BD, BDF_p, DH, AHB_p, BH],
△BEG : [CBE_p, BE, BEG_p, EG, BGE_p, BG],
△BGH : [CBE_p, BG, BGH_p, GH, BHG_p, BH],
△CEG : [DCE_p, CE, AEG_p, EG, BGE_p, CG], #ミスで抜かしていた
△DFG : [FDG_p, DF, AFG_p, FG, BGE_p, DG],
△DGH : [FDG_p, DG, BGH_p, GH, AHG_p, DH],
△EGH : [GEH_p, EG, EGH_p, GH, BHG_p, EH],
△EFH : [GEH_p, EF, EFH_p, FH, AHB_p, EH],
△FGH : [GFH_p, FG, EGH_p, GH, AHB_p, FH]
];
cluster_lst := [
[[A, C, D], [CAD_p, AC, ACD_p, CD, ADB_p, AD]],
[[A, C, G], [CAG_p, AC, ACD_p, CG, AGB_p, AG]],
[[A, E, F], [CAD_p, AE, AEG_p, EF, AFG_p, AF]],
[[A, E, H], [CAD_p, AE, AEH_p, EH, AHB_p, AH]],
[[A, E, G], [CAG_p, AE, AEG_p, EG, AGE_p, AG]],
[[A, D, G], [DAG_p, AD, ADG_p, DG, AGB_p, AG]],
[[A, F, G], [DAG_p, AF, AFG_p, FG, AGE_p, AG]],
[[A, G, H], [DAG_p, AG, AGH_p, GH, AHG_p, AH]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, AEB_p, BE]],
[[B, D, H], [CBE_p, BD, BDF_p, DH, AHB_p, BH]],
[[B, E, G], [CBE_p, BE, BEG_p, EG, BGE_p, BG]],
[[B, G, H], [CBE_p, BG, BGH_p, GH, BHG_p, BH]],
[[C, E, G], [DCE_p, CE, AEG_p, EG, BGE_p, CG]],
[[D, F, G], [FDG_p, DF, AFG_p, FG, BGE_p, DG]],
[[D, G, H], [FDG_p, DG, BGH_p, GH, AHG_p, DH]],
[[E, G, H], [GEH_p, EG, EGH_p, GH, BHG_p, EH]],
[[E, F, H], [GEH_p, EF, EFH_p, FH, AHB_p, EH]],
[[F, G, H], [GFH_p, FG, EGH_p, GH, AHB_p, FH]],
[[A, C, D, G], [CAG_p, AC, ACD_p, CD, CDG_h, DG, AGB_p, AG]],
[[C, E, F, D], [DCE_p, CE, AEG_p, EF, AFG_p, DF, BDF_p, CD]],
[[A, E, H, F], [CAD_p, AE, AEH_p, EH, AHB_p, AF, AFH_h, FH]],
[[C, E, H, D], [DCE_p, CE, AEH_p, EH, AHB_p, DH, BDF_p, CD]],
[[A, C, E, G], [CAG_p, AC, ACD_h, CE, AEG_p, EG, AGE_p, AG]],
[[A, E, F, G], [CAG_p, AE, AEG_p, EF, EFG_h, FG, AGE_p, AG]],
[[A, D, F, G], [DAG_p, AD, ADF_h, DF, AFG_p, FG, AGE_p, AG]],
[[A, G, H, D], [DAG_p, AG, AGH_p, GH, AHG_p, DH, ADF_h, AD]],
[[A, G, H, F], [DAG_p, AG, AGH_p, GH, AHG_p, FH, AFH_h, AF]],
[[C, D, H, E], [DCE_p, CD, BDF_p, DH, AHB_p, EH, AEH_p, CE]],
[[E, B, D, F], [BEG_p, BE, CBE_p, BD, BDF_p, DF, AFE_p, EF]],
[[B, E, G, C], [CBE_p, BE, BEG_p, EG, BGE_p, CG, BCD_h, BC]],
[[B, E, F, D], [CBE_p, BE, BEG_p, EF, AFE_p, DF, BDF_p, BD]],
[[B, D, G, H], [CBE_p, BD, BDG_h, DG, BGH_p, GH, BHG_p, BH]],
[[B, G, H, E], [CBE_p, BG, BGH_p, GH, BHG_p, EH, BEH_h, BE]],
[[C, G, H, E], [DCE_p, CG, BGH_p, GH, BHG_p, EH, AEH_p, CE]],
[[C, E, F, D], [DCE_p, CE, AEG_p, EF, AFE_p, DF, BDF_p, CD]],
[[D, G, H, F], [FDG_p, DG, BGH_p, GH, AHG_p, FH, AFH_h, DF]],
[[E, F, G, H], [GEH_p, EF, EFG_h, FG, EGH_p, GH, BHG_p, EH]]
];
always {
DAG_p == 20; #答えで確認した。紛らわしいが
CBE_p == 50;
BGE_p == 65;
EGH_p == 15;
AHB_p == 30;
ACG_p == DCE_p;
ACD_p == BCE_p;
ADB_p == FDG_p;
ADG_p == BDF_p;
AFE_p == GFH_p;
AFG_p == EFH_p;
AC + CE == AE;
BC + CD == BD;
BC + CG == BG;
AD + DF == AF;
AD + DH == AH;
BD + DG == BG;
CD + DG == CG;
BE + EH == BH;
AF + FH == AH;
DF + FH == DH;
EF + FG == EG;
CAD_p + DAG_p == CAG_p;
AEG_p + GEH_p == AEH_p;
AGB_p + BGE_p == AGE_p;
AGB_p + BGH_p == AGH_p;
AGE_p + EGH_p == AGH_p;
AEB_p + AEG_p == BEG_p;
AHB_p + AHG_p == BHG_p;
BGE_p + EGH_p == BGH_p;
ACB_p + BCE_p == 180;
ACB_p + ACD_p == 180;
ADB_p + BDF_p == 180;
ADB_p + ADG_p == 180;
ABE_p + AEH_p == 180;
BEG_p + GEH_p == 180;
AFE_p + EFH_p == 180;
AFE_p + AFG_p == 180;
}
で、まあ点に着目して確認すると、必要な角の和は取得されてるわけだ。おそらく全体が三角形で構成されていたからだろう。
今回は使わないが、クラスタ内での交点の発生についても考えてみる。
交点さえ考えることができれば、何と何が繋がっているかはgraphにあるので、分割したクラスタもまた分割することができるだろう。
まず2つの辺について考える。
頂点同士から伸びている場合は、同じ頂点から伸びている場合は、交点は発生しない。違う頂点から伸びている場合は、交点は必ず発生する。
頂点から伸びている辺と、辺から辺へ伸びている辺だと、頂点を挟む辺同士で発生している辺だと、必ず交点は発生する。底辺が関わる場合、底辺における2つの辺の位置関係で、交点ができる場合とできない場合の2通りが考えられる。
辺から辺へ伸びている辺同士の場合は、もしその辺が同じ端点を共有している場合は、交点は絶対に発生しない。
また、(三角形の)2辺で完結する場合は、その2辺の間で点と点の位置関係を見れば良い。
(三角形の)3辺が関わる場合も、2つがくっついている辺と、1つずつしかくっついていない辺の、位置関係を見れば良い。
2つの辺の場合は簡単だが、3つの辺が絡んでくると、交点が発生する際の位置関係が難しくなるのではないか。
三角関数?が必要なんじゃないかなあ。そうすると、平面が概念として必要になるのではないか。同一平面上にある点同士で無ければ、そもそも三角関数?は成立しないだろう。交点ができるとしたらどこかを判定することはできるが、いや、それならクラスタの中であれば必要無いのか。
まあ、辺における点の前後関係自体は、graphにおいて、まず片方に点が何も無いのを探して、次にその一つ前だけがあるのを探して、というのを続ければ良いと思うけど。そういう位置関係が曖昧なのは、そもそも入れないとして。いや、入れるんだっけな?まあ実際に詳しくやってみないと分からないが。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その21
ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。交点の確認はこの方法を使う。
06年度トライアル問題 問題9
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
 』
』
最終的な目標はプログラミングみたいに記述することなんだが、まあ前みたいにできるまで繰り返そうと思う。まずは全体の流れをハッキリさせてからだろう。
ちなみに、現在の問題点は2つで、一つは問題文の記述で、ネガティブな角を含むクラスタが情報として必要になる問題がこれから出てくるか。
もう一つは、角の和を取得する方法にクラスタがあるが、クラスタを見つけるには角の和が必要なこと。言い換えれば、主に辺の和から1つの点に辺が伸びている以外に、角の和を取得する方法は無いのかだ。
では、初期条件。
graph := [
A : [
[[B], []],
[[D], []]
]
,
B : [
[[A], []],
[[C], []]
]
,
C : [
[[B], []],
[[D], []]
]
,
D : [
[[A], []],
[[C], []]
]
];
parallel_lines_lst := [
];
triangle_lst := [
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]]
];
always {
ABC_p == 168;
BCD_p == 108;
AB == BC == CD;
}
まずは角のイコールを確認する。
parallel_lines_lstには何も無い。
graphを確認して、どのkeyのvalueも2つ以上の、[0]も[1]も「!= 」のが無いので、対頂角は無し。valueの順番が関係無い組み合わせで確認したいのだけど、まあできる機能はあるだろう。
辺のイコールは定義どおりなので、新しく確認はしない。
辺の和を確認する。
graphを確認して、それぞれvalueの中身をfor文で調べて、[0]と[1]が「!= 」だったら、その[0]と[1]のそれぞれのfor文の組み合わせで、辺の和を追加していく。
triangle_lstを更新する。
graphを確認して、keyのvalueの中身で更にgraphを確認し、その中にkeyのvalueの中身と同じものがあれば、それらは三角形だ。
graphに着目して、辺にそのまま辺が当たっていて、足したら180°になるものを辺の和として登録する。
三角形に着目して、辺が更に反対側に伸びていたら、外角として登録する。
辺の和とtriangle_lstに着目して、もう一方の点が共有されていたら、登録する。
cluster_lstを更新する。
三角形はそのまま登録する。
更にクラスタ同士で辺を共有していて
それが三角形で直線で繋がっていたら、クラスタ
「角の一方 + 角のもう一方 == それらの角の共有していない辺同士の角 and それらの角の共有していない辺同士の角 <= 180」だったら、クラスタ
クラスタだと分かった後の角の和だとかの判定方法も詳しく考える必要がある。
いや、全体の流れをハッキリさせることに集中することにした。
「全体の話」
・記録1だとかで後戻りする
・アルゴリズムクイックリファレンスを参考にする
・答えを調べて達しているか
「点と点を結んで線にする」
graphを調べて、繋がっていないkeyと繋ぐ
・既存の角を割る動作でもあるはず
全ての辺と辺の角の、ポジティブかネガティブを割る。
クラスタを確認して、あれば、ポジティブを割っている
割ったのがポジティブなら、生まれるのもポジティブ
割った角がポジティブかネガティブか分からない時は、alwaysに条件式を作って、分かり次第確定するようにする
・三角形リストも調べることで更新する
・交点の判断は、クラスタ以外では三角関数が無ければ分からないのでは
「点と点の距離の分だけ線を延長」
graphを調べていって、辺のもう片方が無ければ、延長できる
・追加する点はアルファベット順に
・元々の辺がクラスタの一部なら、割る辺はネガティブ。結果は180とポジティブ
・イコールなので定義も追加する
・そういえば、辺の和も追加する必要があるな
・「手元で簡単に、1点から3辺が伸びている図を描いてみると、そういうのが3種類発生するはず
"BAD_p" + "DAE_p" == "BAE_h";
"BAD_p" + "BAE_h" == "DAE_n";」
・交点の判断は三角関数
「2点と、その間の垂直線とどこか1辺の交点による、二等辺三角形の作図」
三角形を調べていく
・追加する点はアルファベット順に
・2角を調べて、角度が小さい方と交わる。1つの三角形で3通り発生する
・「if "ABD_p" > "BAD_p" {~~~} elif ~~~」という具合か。
・「"BAD_p" + "ADB_p" + 132 == 180」から、「"BAD_p" < 48」を出せれば良いが。
・graphを更新する
・クラスタとして分割する
割る角はポジティブ
cluster_lst
・定義を追加する
・クラスタも調べれるが、とりあえずは調べない
「ある1辺と同じ長さの辺を別の辺に落とすことによる二等辺三角形の作図」
三角形を調べていく
・追加する点はアルファベット順に
・2角を調べて、両方が90°以下の時に
・今度は角度が大きい方の辺で作れるのでは。1つの三角形で3通り確認する
「クラスタの貼り合わせ」
クラスタを調べていく
・同じ長さの辺があれば
・それに対応するように複製し
・その重ね合わせる所にそのまま入り込むように、逆にしたり循環させたり
・重なり合う角の足し算がそれぞれポジティブであれば、そのままクラスタに登録
で、問題はやはり、クラスタと角の和と交点。
平面という概念があると、いわゆる何が嬉しいか、を考えると、まず角の和を考える時に、2つの角の1辺が隣接していたとして、「隣接していない辺同士の角 > 一方の角 and 隣接していない辺同士の角 > もう一方の角」で、判定できることだろう。平面という概念が無ければ、「隣接していない辺同士の角 == 一方の角 + もう一方の角」である必要がある。
あと、これは今朝気付いたんだが、三角関数を判定する時に、3Dだと上の角度以外の全ての情報が揃っていても、交点が発生するか考えることができないのではないか。
(あとは、四角形のクラスタかを判定する時に、繋がっている全ての辺を底辺と捉えて三角形で無ければ、全ての角がポジティブな四角形のクラスタだと言える。)
この2つの点で障害というか必要性が出れば、やはり平面という概念を導入することになるだろう。
その平面の嬉しさを抜きにしてネガティブな角を持つクラスタを考えると、区切って全ての角がポジティブだったら普通のクラスタだと見なせるというような、クラスタの前段階のようなものになるんじゃないか。そういう問題に出くわさないと分からないが。
角の和は、一辺を共有していて、「隣接していない辺同士の角 == 一方の角 + もう一方の角」という、つまりクラスタの片方バージョンのような条件というか定義になるわけだが、これ自体が角の和を含んでいるわけで、クラスタで角から辺に伸びていた時だとかに、クラスタから角の和という順番で考えるだけで良いのではないか。
あと、やっぱり圧倒的に問題のサンプルが足りていないという感じがしている。他の問題でも、必要な角の和が初期状態から弾き出せるのか試してみるつもりだ。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その20
ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。交点の確認はこの方法を使う。
03年度ファイナル問題 問題2
『右の図の四角形ABCDと四角形EFCGは合同な平行四辺形で、辺EGを延長した線は点Dを通り、辺CBを延長した線は点Eを通ります。
このとき、角BACの[ア]倍と角CADの[イ]倍の和は180度となります。
[ア]、[イ]に入る整数をそれぞれ答えなさい。
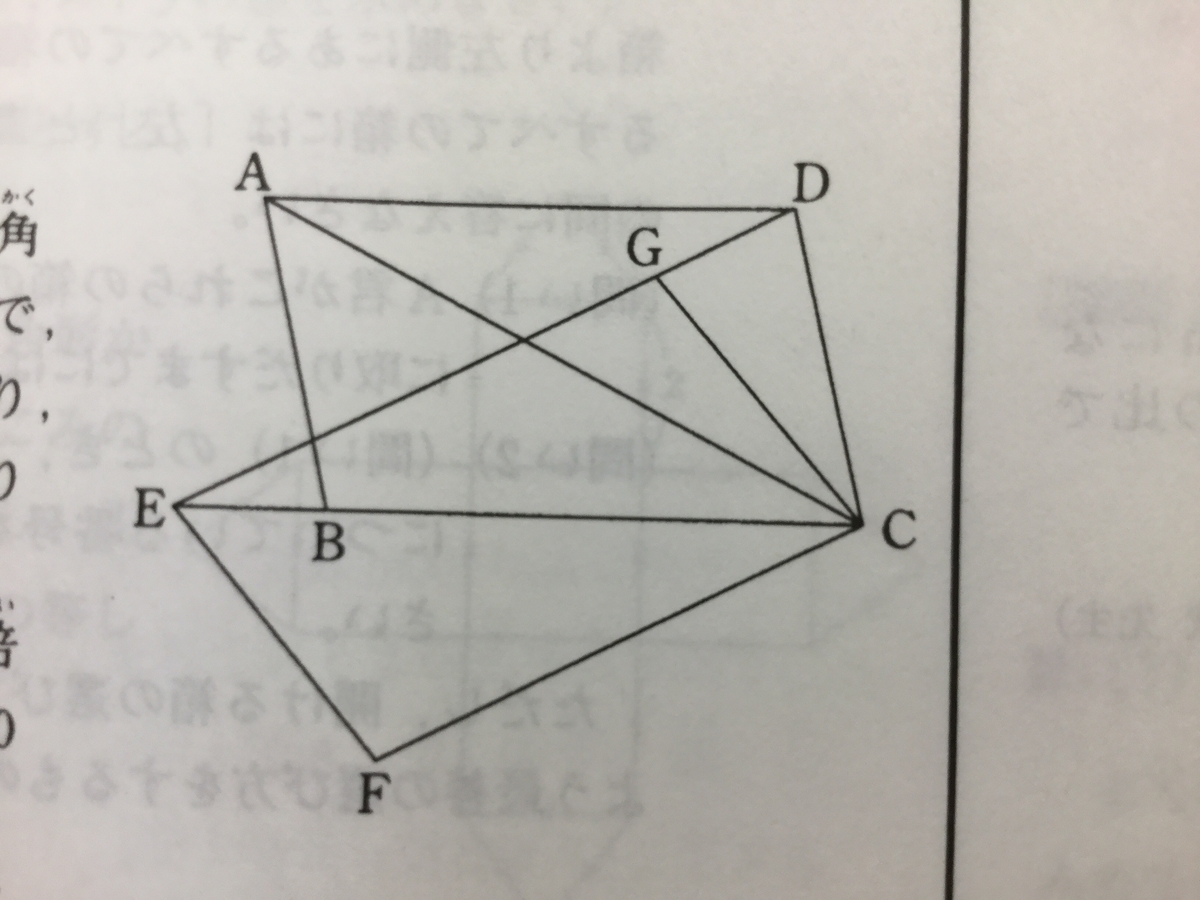 』
』
前回の続き。最近は自動化におけるデータの移り変わりを手作業でやってみている。
初期入力はできるだけ、graph、adjacent_angle_lst(名称を元に戻した)、の2つから立ち上げて、cluster_lstはどの程度必要なのか探っていきたい。まあもちろん、それ以外にも何と何がイコールかだとか、今回だと平行線を登録する必要があるわけだが、主眼はそこのつもりだ。
名付けられていない交点を、上からH、Iと名付ける。
graph := [
A : [
[[B, I], []],
[[C, H], []],
[[D], []]
]
,
B : [
[[A, I], []],
[[C], [E]]
]
,
C : [
[[A, H], []],
[[B, E], []],
[[D], []],
[[F], []],
[[G], []]
]
,
D : [
[[A], []],
[[C], []],
[[E, G, H, I], []]
]
,
E : [
[[B, C], []],
[[D, G, H, I], []],
[[F], []]
]
,
F : [
[[C], []],
[[E], []]
]
,
G : [
[[C], []],
[[D], [E, H, I]]
]
,
H : [
[[A], [C]],
[[D, G], [E, I]]
]
,
I : [
[[A], [B]],
[[D, G, H], [E]]
]
];
adjacent_angle_lst := [ #[0] + [1] == [2]。隣接を足し算で表現してみた
[BAC_p, CAD_p, BAD_p], #平行四辺形だからポジティブと判断できる、がそれも自動化すべきなのか?
[BAC_p, BAD_n, CAD_n],
[CAD_p, BAD_n, BAC_n],
[ABE_p, ABC_p, CBE_h],
[ABE_p, CBE_h, ABC_n],
[ABC_p, CBE_h, ABE_n],
[ACB_p, ACG_p, BCG_p],
[ACG_p, DCG_p, ACD_p],
[DCG_p, DCF_1, FCG_n],
[DCF_1, BCF_p, BCD_n],
[BCF_p, ACB_p, ACF_p],
[BCG_p, DCG_p, BCD_p],
[BCG_p, BCF_p, FCG_p],
[ACD_p, DCF_1, ACF_n],
[ACD_p, ACB_p, BCD_p],
[FCG_n, ACG_p, ACF_n],
[FCG_n, BCF_p, BCG_n],
[BCD_n, DCG_p, BCG_n],
[BCD_n, ACB_p, ACD_n],
[ACF_p, ACG_p, FCG_p],
[ACF_p, DCF_1, ACD_n],
[BCG_p, FCG_n, BCF_n],
[BCG_p, BCD_n, DCG_n],
[ACD_p, BCD_n, ACB_n],
[ACD_p, ACF_p, DCF_2],
[FCG_n, ACF_p, ACG_n],
[FCG_n, BCG_p, BCF_n],
[BCD_n, BCG_p, DCG_n],
[BCD_n, ACD_p, ACB_n],
[ACF_p, FCG_n, ACG_n],
[ACF_p, ACD_p, DCF_p],
~~~~~~~~~~~~~~~~
];いや駄目だ。どんなに論理的に正しくても、入力したくない。どうにかグラフから自動化しよう。
…そもそも、隣り合うとは何だろうか。辺と辺を1本の辺で共有するだけで無く、もう一方側の点と点の関係も問わなければいけないのではないか。
もう一方側の点と点で三角形を作って、その頂点が、隣り合っていると言われる二つの角の和になった時に、初めて隣り合っていると言えるのではないか。
クラスターも、ネガティブなものは考えないようにしよう。クラスターの、ネガティブな辺と辺を貼り合わせるというのは、問題としてありそうにない。
一方で、クラスターは拡大でなく、やはり平面的に貼り合わせていると考えることにしよう。1角が90°以上の三角形の角同士を貼り合わせる必要がある問題は、いかにもありそうだ。その時に、角の和がそれぞれ180°以下だったら、クラスターとして登録する。
graph → triangle_lst → cluster_lst、という順番で展開していこう。
この問題においては、平行線を登録しておけば、それだけで平行四辺形の分はクラスタとして登録される。それで結果的に、この問題の角の和は弾き出すことができる。
直線を二分した場合は、そのまま角の和として登録しよう。また、1辺を共有する三角形同士が、もう一方の点・共有する辺の底辺側の点・もう一方の点、という風に直線で繋がっている時にも、クラスタや角の和として登録しよう。
じゃあ一回やってみようかな。
graph := [
A : [
[[B, I], []],
[[C, H], []],
[[D], []]
]
,
B : [
[[A, I], []],
[[C], [E]]
]
,
C : [
[[A, H], []],
[[B, E], []],
[[D], []],
[[F], []],
[[G], []]
]
,
D : [
[[A], []],
[[C], []],
[[E, G, H, I], []]
]
,
E : [
[[B, C], []],
[[D, G, H, I], []],
[[F], []]
]
,
F : [
[[C], []],
[[E], []]
]
,
G : [
[[C], []],
[[D], [E, H, I]]
]
,
H : [
[[A], [C]],
[[D, G], [E, I]]
]
,
I : [
[[A], [B]],
[[D, G, H], [E]]
]
];
triangle_lst := [
];
cluster_lst := [
];
parallel_lines_lst := [ #どうやって表現しようかな。ADとCE、ABとCD、DEとCF、EFとCG、なんだけど。例えば。
[[A, D], [E, B, C]],
[[A, I, B], [D, C]],
[[D, G, H, I, E], [C, F]],
[[E, F], [G, C]]
];
always {
AD == BC;
AB == CD;
BAD_p == BCD_p;
ADC_p == ABC_p;
EG == CF;
EF == CG;
DEF_p == FCG_p;
CGE_p == CFE_p;
AD == EG; #やや手抜き
EF == AB;
BAD_p == DEF_p;
ADC_p == CGE_p;
}
ここからスタート。で、triangle_lstを更新。ある点と繋がっている点が更に別の繋がっている点と繋がっているか。
点に着目して対頂角でのイコールを登録。点に着目して辺の和も登録。
graph := [
A : [
[[B, I], []],
[[C, H], []],
[[D], []]
]
,
B : [
[[A, I], []],
[[C], [E]]
]
,
C : [
[[A, H], []],
[[B, E], []],
[[D], []],
[[F], []],
[[G], []]
]
,
D : [
[[A], []],
[[C], []],
[[E, G, H, I], []]
]
,
E : [
[[B, C], []],
[[D, G, H, I], []],
[[F], []]
]
,
F : [
[[C], []],
[[E], []]
]
,
G : [
[[C], []],
[[D], [E, H, I]]
]
,
H : [
[[A], [C]],
[[D, G], [E, I]]
]
,
I : [
[[A], [B]],
[[D, G, H], [E]]
]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△ADI : [BAD_p, AD, ADE_p, DI, AID_p, AI],
△AHI : [ABC_p, AH, AHE_p, HI, AID_p, AI],
△ACD : [CAD_p, AC, ACD_p, CD, ADC_p, AD],
△ADH : [CAD_p, AD, ADE_p, DH, AHD_p, AH],
△BEI : [ABE_p, BE, BED_p, EI, BIE_p, BI],
△CDH : [ACD_p, CD, CDE_p, DH, CHD_p, CH],
△CGH : [BCG_p, CG, CGE_p, GH, CHD_p, CH],
△CEH : [ACB_p, CE, BED_p, EH, CHE_p, CH],
△CDE : [BCD_p, CD, CDE_p, DE, BED_p, CE],
△CEG : [BCG_p, CE, BED_p, EG, CGE_p, CG],
△CEF : [BCF_p, CE, BEF_p, EF, CFE_p, CF],
△CDG : [DCG_p, CD, CDE_p, DG, CGD_p, CG]
];
cluster_lst := [
];
parallel_lines_lst := [ #どうやって表現しようかな。ADとCE、ABとCD、DEとCF、EFとCG、なんだけど。例えば。
[[A, D], [E, B, C]],
[[A, I, B], [D, C]],
[[D, G, H, I, E], [C, F]],
[[E, F], [G, C]]
];
always {
AD == BC;
AB == CD;
BAD_p == BCD_p;
ADC_p == ABC_p;
EG == CF;
EF == CG;
DEF_p == FCG_p;
CGE_p == CFE_p;
AD == EG; #やや手抜き
EF == AB;
BAD_p == DEF_p;
ADC_p == CGE_p;
AHD_p == CHE_p;
AHE_p == CHD_p;
AID_p == BIE_p;
AIE_p == BID_p;
BC + BE == CE;
DG + EG == DE;
DG + GH == DH;
DG + GI == DI;
AH + CH == AC;
DH + EH == DE;
DH + HI == DI;
GH + EH == EG;
GH + HI == GI;
AI + BI == AB;
DI + EI == DE;
GI + EI == EG;
HI + EI == EH;
}
平行線のセットの一方を一つ一つ確認して、何とか更新。クラスターもついでに更新した。
graph := [
A : [
[[B, I], []],
[[C, H], []],
[[D], []]
]
,
B : [
[[A, I], []],
[[C], [E]]
]
,
C : [
[[A, H], []],
[[B, E], []],
[[D], []],
[[F], []],
[[G], []]
]
,
D : [
[[A], []],
[[C], []],
[[E, G, H, I], []]
]
,
E : [
[[B, C], []],
[[D, G, H, I], []],
[[F], []]
]
,
F : [
[[C], []],
[[E], []]
]
,
G : [
[[C], []],
[[D], [E, H, I]]
]
,
H : [
[[A], [C]],
[[D, G], [E, I]]
]
,
I : [
[[A], [B]],
[[D, G, H], [E]]
]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△ADI : [BAD_p, AD, ADE_p, DI, AID_p, AI],
△AHI : [ABC_p, AH, AHE_p, HI, AID_p, AI],
△ACD : [CAD_p, AC, ACD_p, CD, ADC_p, AD],
△ADH : [CAD_p, AD, ADE_p, DH, AHD_p, AH],
△BEI : [ABE_p, BE, BED_p, EI, BIE_p, BI],
△CDH : [ACD_p, CD, CDE_p, DH, CHD_p, CH],
△CGH : [BCG_p, CG, CGE_p, GH, CHD_p, CH],
△CEH : [ACB_p, CE, BED_p, EH, CHE_p, CH],
△CDE : [BCD_p, CD, CDE_p, DE, BED_p, CE],
△CEG : [BCG_p, CE, BED_p, EG, CGE_p, CG],
△CEF : [BCF_p, CE, BEF_p, EF, CFE_p, CF],
△CDG : [DCG_p, CD, CDE_p, DG, CGD_p, CG]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[A, D, I], [BAD_p, AD, ADE_p, DI, AID_p, AI]],
[[A, H, I], [ABC_p, AH, AHE_p, HI, AID_p, AI]],
[[A, C, D], [CAD_p, AC, ACD_p, CD, ADC_p, AD]],
[[A, D, H], [CAD_p, AD, ADE_p, DH, AHD_p, AH]],
[[B, E, I], [ABE_p, BE, BED_p, EI, BIE_p, BI]],
[[C, D, H], [ACD_p, CD, CDE_p, DH, CHD_p, CH]],
[[C, G, H], [BCG_p, CG, CGE_p, GH, CHD_p, CH]],
[[C, E, H], [ACB_p, CE, BED_p, EH, CHE_p, CH]],
[[C, D, E], [BCD_p, CD, CDE_p, DE, BED_p, CE]],
[[C, E, G], [BCG_p, CE, BED_p, EG, CGE_p, CG]],
[[C, E, F], [BCF_p, CE, BEF_p, EF, CFE_p, CF]],
[[C, D, G], [DCG_p, CD, CDE_p, DG, CGD_p, CG]]
];
parallel_lines_lst := [ #どうやって表現しようかな。ADとCE、ABとCD、DEとCF、EFとCG、なんだけど。例えば。
[[A, D], [E, B, C]],
[[A, I, B], [D, C]],
[[D, G, H, I, E], [C, F]],
[[E, F], [G, C]]
];
always {
AD == BC;
AB == CD;
BAD_p == BCD_p;
ADC_p == ABC_p;
EG == CF;
EF == CG;
DEF_p == FCG_p;
CGE_p == CFE_p;
AD == EG; #やや手抜き
EF == AB;
BAD_p == DEF_p;
ADC_p == CGE_p;
AHD_p == CHE_p;
AHE == CHD_p;
AID_p == BIE_p;
AIE_p == BID_p;
BC + BE == CE;
DG + EG == DE;
DG + GH == DH;
DG + GI == DI;
AH + CH == AC;
DH + EH == DE;
DH + HI == DI;
GH + EH == EG;
GH + HI == GI;
AI + BI == AB;
DI + EI == DE;
GI + EI == EG;
HI + EI == EH;
BAD_p == ABE_p;
CAD_p == ACB_p;
ADE_p == BED_p;
BAC_p == ACD_p;
AID_p == CDE_p;
BIE_p == CDE_p;
ABE_p == BCD_p;
CGD_p == GCF_p;
CHD_p == ACF_p;
AHE_p == ACF_p;
CED_p == ECF_p;
DEF_p == CGD_p;
CEF_p == BCG_p;
}
ここまでは予定通りで、このまま三角形定理ループを回すこともできる。ただ問題はここからで、角の和を弾き出す必要がある。
まず、点に着目して、辺にそのまま辺が当たっていて、足したら180°になるような分かれ方をしているのを探す。
あと、三角形に着目して外角による足し算も更新していく。
更には、これがメインなわけだが、2点を共有しているような三角形で、そうじゃない点同士が共有しているどちらか1点を挟んで直線だったら、共有しているもう一方の点の角の和を登録していく。
graph := [
A : [
[[B, I], []],
[[C, H], []],
[[D], []]
]
,
B : [
[[A, I], []],
[[C], [E]]
]
,
C : [
[[A, H], []],
[[B, E], []],
[[D], []],
[[F], []],
[[G], []]
]
,
D : [
[[A], []],
[[C], []],
[[E, G, H, I], []]
]
,
E : [
[[B, C], []],
[[D, G, H, I], []],
[[F], []]
]
,
F : [
[[C], []],
[[E], []]
]
,
G : [
[[C], []],
[[D], [E, H, I]]
]
,
H : [
[[A], [C]],
[[D, G], [E, I]]
]
,
I : [
[[A], [B]],
[[D, G, H], [E]]
]
];
triangle_lst := [
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△ADI : [BAD_p, AD, ADE_p, DI, AID_p, AI],
△AHI : [BAC_p, AH, AHE_p, HI, AID_p, AI],
△ACD : [CAD_p, AC, ACD_p, CD, ADC_p, AD],
△ADH : [CAD_p, AD, ADE_p, DH, AHD_p, AH],
△BEI : [ABE_p, BE, BED_p, EI, BIE_p, BI],
△CDH : [ACD_p, CD, CDE_p, DH, CHD_p, CH],
△CGH : [BCG_p, CG, CGE_p, GH, CHD_p, CH],
△CEH : [ACB_p, CE, BED_p, EH, CHE_p, CH],
△CDE : [BCD_p, CD, CDE_p, DE, BED_p, CE],
△CEG : [BCG_p, CE, BED_p, EG, CGE_p, CG],
△CEF : [BCF_p, CE, BEF_p, EF, CFE_p, CF],
△CDG : [DCG_p, CD, CDE_p, DG, CGD_p, CG]
];
cluster_lst := [
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[A, D, I], [BAD_p, AD, ADE_p, DI, AID_p, AI]],
[[A, H, I], [ABC_p, AH, AHE_p, HI, AID_p, AI]],
[[A, C, D], [CAD_p, AC, ACD_p, CD, ADC_p, AD]],
[[A, D, H], [CAD_p, AD, ADE_p, DH, AHD_p, AH]],
[[B, E, I], [ABE_p, BE, BED_p, EI, BIE_p, BI]],
[[C, D, H], [ACD_p, CD, CDE_p, DH, CHD_p, CH]],
[[C, G, H], [BCG_p, CG, CGE_p, GH, CHD_p, CH]],
[[C, E, H], [ACB_p, CE, BED_p, EH, CHE_p, CH]],
[[C, D, E], [BCD_p, CD, CDE_p, DE, BED_p, CE]],
[[C, E, G], [BCG_p, CE, BED_p, EG, CGE_p, CG]],
[[C, E, F], [BCF_p, CE, BEF_p, EF, CFE_p, CF]],
[[C, D, G], [DCG_p, CD, CDE_p, DG, CGD_p, CG]]
];
parallel_lines_lst := [ #どうやって表現しようかな。ADとCE、ABとCD、DEとCF、EFとCG、なんだけど。例えば。
[[A, D], [E, B, C]],
[[A, I, B], [D, C]],
[[D, G, H, I, E], [C, F]],
[[E, F], [G, C]]
];
always {
AD == BC;
AB == CD;
BAD_p == BCD_p;
ADC_p == ABC_p;
EG == CF;
EF == CG;
DEF_p == FCG_p;
CGE_p == CFE_p;
AD == EG; #やや手抜き
EF == AB;
BAD_p == DEF_p;
ADC_p == CGE_p;
AHD_p == CHE_p;
AHE == CHD_p;
AID_p == BIE_p;
AIE_p == BID_p;
BC + BE == CE;
DG + EG == DE;
DG + GH == DH;
DG + GI == DI;
AH + CH == AC;
DH + EH == DE;
DH + HI == DI;
GH + EH == EG;
GH + HI == GI;
AI + BI == AB;
DI + EI == DE;
GI + EI == EG;
HI + EI == EH;
BAD_p == ABE_p;
CAD_p == ACB_p;
ADE_p == BED_p;
BAC_p == ACD_p;
AID_p == CDE_p;
BIE_p == CDE_p;
ABE_p == BCD_p;
CGD_p == GCF_p;
CHD_p == ACF_p;
AHE_p == ACF_p;
CED_p == ECF_p;
DEF_p == CGD_p;
CEF_p == BCG_p;
ABC_p + ABE_p == 180;
CGD_p + CGE_p == 180;
AHD_p + AHE_p == 180;
AID_p + AIE_p == 180;
BAC_p + ACB_p == ABE_p;
BAD_p + ADE_p == AIE_p;
BAD_p + ADE_p == BID_p; #同じ角に二つある場合は対頂角なので次回からは省く
BAC_p + AID_p == AHD_p;
BAC_p + AHE_p == AIE_p;
CAD_p + ADE_p == AHE_p;
BED_p + BIE_p == ABC_p;
ABE_p + BED_p == AIE_p;
ACD_p + CDE_p == CHE_p;
ACG_p + CHD_p == CGD_p;
ACG_p + CGE_p == AHD_p;
ACB_p + BED_p == CHD_p;
BCG_p + BED_p == CGD_p;
DCG_p + CDE_p == CGE_p;
DCG_p + BCG_p == ACD_p; #CDG, CGH
DCG_p + BCG_p == BCD_p; #CDG, CEG
ADH_p + CDH_p == ADC_p; #ADH, CDH
DCH_p + ECH_p == BCD_p; #CDH, CEH
CAD_p + BAC_p == BAD_p; #ADH, AHI
BCG_p + ACB_p == ACG_p; #CGH, CEH
}いや大変だった。今振り返ると、辺の和に着目したら良かったのかな?
で、こうなって一つ一つ見てみると、点Fが絡む角の和が登録されていないことが分かる。
まず、GとFに辺を引く作画をする。そうすると、例えば角DEF全体が錯角だとかで180-CFEだと分かる。で、まあその角があるような三角形CEFを見ると、180-角CFEの残りの2角が、錯角だとかでDEFを構成する2つの角だと分かる。
クラスタ同士で辺を共有するものを探し、更に頂点同士でもう一対のクラスタも探し、角の和が頂点と頂点の角と同じになっているような、かな?
更に、DとFに辺を引く作画をする。
…これは、まずDが一つ前のクラスタの外側にあることは分かる。直線で伸ばしているので外側だし、そちら側は180°なので、クラスタとしての条件はクリアしている。
問題は逆側で、どう考えれば良いのかなあ。どちら側も180°だったら四角形になってしまうので、という説明では駄目だろうか。どちらかが180°だったら、繋げるのが三角形だったら180°以下だ。
そうすると、クラスタの拡大に成功して、DからFは角を割っているし、CからGも角を割っていて、しかもクラスタの順番的に交点が発生して、みたいな感じ。
しかし、今回は良かったけど、意外と足し算として成立させるのは難しいのかもしれないな。
いや、今回は、CDGFにおいて、三角形CDGと三角形CFG(順番は対応しておらず)は相似形で、角CGF + 角DFG == 角CDF + 角DCG == を仮に?1としてみる。あと、?1 + 相似形の底辺2角 == 180。
そうすると、元々CGD == FCGで、角DCGが?1 - 角CDFなので、って感じで行けないだろうか。無理だろうか。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その19
ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。交点の確認はこの方法を使う。
06年度トライアル問題 問題9
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
 』
』
前回の続き。今日は細々とした考察を進めていく。
クラスタについて
二等辺三角形の作図など、他の作図はわりとハッキリしはじめているのだけど、クラスタの作図はまだ全然なので、その考察をする。
まず、クラスタという機能に何を求めているのか、を考えると、まずはこの問題を解くのにその機能がいる。そして、(2次元上のユークリッド幾何の問題において)角の和について登録する時にクラスタという概念がいる。
前者は場当たり的に満たしていけば良い、つまり、できる限り最小の実装をして、必要であれば機能を拡張していけば良い。
そして後者について考えると、このクラスタには全ての角がp(ポジティブ、つまり2辺でできる2つの角のうちの180°以下の方)じゃないものは加えない方が良いのではないか。
三角形はクラスタ(面のこと)で、三角形の底辺を合わせて、その底辺が耐震構造のバッテンのようになるように交わるように、四角形を作った時に、その四角形はクラスタだと見なせるという話だった(説明が下手くそで申し訳ない)。
三角形の底辺を合わせて、その一方の合わさった角と、それぞれの頂点で三角形を作っただけで良いんじゃないか、と思ったこともあった。しかしその場合だと、もう一方の合わさった角がネガティブな場合もあり得る。それだと角の和を考える時には不都合なわけだ。
問題は、問題文の図を写す時にそれでは記述できない場合があることで、それについてはどう考えれば良いのかな。
クラスタを合体する作図の時には、合わせた辺でできる角の和がそれぞれポジティブであれば良いわけだが。
まあしかし、角の和を考える時に、面を想定する以外に方法ってあるのかな。点と、角と角の向き合い方だけに着目するっていうのが構想というかイメージとしてはあるのだけど。
とりあえず、この方針で行って、他の良い方法を思いついたらその方法を採用するということにしようかな。
いやでも、ネガティブな角を生み出している出っ張りの部分を区切るように線を引いた所で、またできる角もネガティブかもしれないんだよな。問題文での図の表現をそのまま写すということを考えると、やっぱりネガティブもクラスタに含めた方が良いのか?
角の隣接というのがキーになると思うんだよな。足し算による隣接の表現を仮に機能として想定してみるか?
四角形に三角形をくっつけたとして、隣接する点の両方と、四角形を作るような処理ができれば、とりあえず多角形の全ての角がポジティブな面というのは、考えることができるんだがな。それでは問題文の図を写せないという点で問題で。
人間の思考をエミュレートする上でどうするのが自然なのかという問題なんだよな。
結局、問題文やその図が論理的に、それも三次元の問題に適用可能な意味で何を表しているのか、が問題なんだよな。それを十分に汲み取れる形式を考えれば良いわけで。
と考えると、何と何が繋がっているかを表すグラフと、何と何が平面として繋がっていてそれぞれの角が少なくともポジティブかネガティブかを表すクラスタ、また遠隔で何と何が同じかを表す式だけで無く、どの角とどの角が隣接しているかを表す機能も当然必要なんじゃないか(ちなみに三角形のリストはグラフから自動生成できる、が一々自動生成するのは面倒なので空のリストというか辞書は作っておくが)。そうじゃないと意味を十分に汲み出したとは言えないんじゃないか。
じゃあ、やっぱり隣接する角を和で表す機能は少なくとも想定することにするか。クラスタを2種類用意するか、はまだ保留なわけだが。
仮に、「adjacent_angle_lst」、としてみようか。
クラスタは今まで通りの「cluster_lst」と、全ての角がポジティブな「p_cluster_lst」で分けて、統合できそうなら統合するか?そうしてみようか。
adjacent_angle_lstは、cluster_lstで代用可能なんじゃないかなあ。別にどちらでも良いのだろうけど、triangle_lstもp_cluster_lstも全部普通のcluster_lstで扱って、そこから3つだけとか、ポジティブな角だけとかで、抽出してもとりあえず問題は無さそうだがな。
いや、adjacent_angle_lstがcluster_lstで代用できるのかっていうのは怪しいな、やってみないと。
graph、adjacent_angle_lst、cluster_lstの3つで行こうか。
ちょっと今日の考察はあまりにもグダグダで申し訳ないのだけど、問題文の図を純粋に眺めてみると、adjacent_angle_lstと、graphと、角や辺や具体的な数値のイコールだけなんだよな。それらの入力から、triangle_lstはもちろん、cluster_lstやp_cluster_lstも生成できないかな。それをどう使うかは後から決めれば良い話で、そういえば平行線のリストもあるはずだし。
いややっぱり駄目だ、この問題が解けねえ。じゃあやっぱりそれプラスでcluster_lstだな。
graphは今までにもあるし、adjacent_angles(名称変更)も角の和を登録する作業として今までも似たようなことをやっていた。cluster_lstでどれだけ登録する必要があるのかが今悩んでいる所で、外側だけで良いのか、それとも全部登録する必要があるのか、全部登録する必要があるとして自動化できるのか(?)。
いや、混乱している。三角形定理ループを自動化した時の例題で、graphとadjacent_angles(と平行線リスト)でどれだけ立ち上げることができるのか、どれだけcluster_lstが必要なのかを試してみようかと思っている。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その18
ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。交点の確認はこの方法を使う。
06年度トライアル問題 問題9
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
 』
』
前回の続きで2ステップ目だけど、クラスタの外から作図した時にどうなるかを見てみたい。なので、1ステップ目はABをB側に延長して、それから2ステップ目をいろいろ試していく。
作図
以下5種類の作図をしていく。直接作図したもの以外に三角形や、あるいは正四角形や正五角形ができていたら、次の定理ループで角度が明らかになる可能性がある。
- 点と点を結んで線にする
- 点と点の距離の分だけ線を延長
- 2点と、その間の垂直線とどこか1辺の交点による、二等辺三角形の作図
- ある1辺と同じ長さの辺を別の辺に落とすことによる二等辺三角形の作図
- クラスタ(面?)とクラスタを繋げてクラスタの拡大(同じ長さの辺の所に)
- 正四角形
- 正五角形
じゃあ、初期状態。
graph := [
"A" : [
[["B"], []],
[["D"], []]
]
,
"B" : [
[["A"], []],
[["C"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A"], []],
[["C"], []]
]
];
triangle_lst := [
];
cluster_lst := [ #shape_lst?
[["A", "B", "C", "D"], ["BAD_p", "AB", "ABC_p", "BC", "BCD_p", "CD", "ADC_p", "DA"]]
];
always {
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
}
じゃあABと同じ長さをB側に作図。新しい点はE。
graph := [
A : [
[[B, E], []],
[[D], []]
]
,
B : [
[[A], [E]],
[[C], []]
]
,
C : [
[[B], []],
[[D], []]
]
,
D : [
[[A], []],
[[C], []]
]
,
E : [
[[A, B], []]
]
];
triangle_lst := [
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, DA]]
];
always {
ABC_p == 168;
BCD_p == 108;
AB == BC == CD;
ABC_p + ABC_n == 360;
BCD_p + BCD_n == 360;
BAD_p + BAD_n == 360;
ADC_p + ADC_n == 360;
AB == BE;
CBE_p + ABE_h == ABC_n;
ABE_h == 180;
CBE_p + CBE_n == 360;
CBE_p + ABC_p == ABE_h;
ABE_h + ABC_p == CBE_n;
}hっていうのを導入した。ハーフ。pとnの反転がよくあるけど、180だったら意味無いんで、仮に。
これ、あらかじめ、「~~~_p < 180」で、「~~~_p + ~~~_n == 360」で、っていうのをalwaysの上の方に定義できないかな。いちいち入れてった方が良いのかな。
あと今気付いたけど、「"AB" == "BE"」とかで無く、「AB == BE」では?文字列の比較になっていて、これマズいよな。直した。まあ元々、集合とか存在の類だし、こちらの方が意味的には純化したと言えるだろう。名前も参照できるようにしよう。
じゃあ、2ステップ目の作図。
まず、点と点を繋げる作図。新しく作ったEと他の点を繋げる。CとDで迷うが、Cは予測がつくので、Dにしよう。
graphを更新。
で、新しく作ったDEと他の辺、例えばBCが交点を持つかだけど、これは三角関数?が無いと分からないんじゃないか。
その辺とその辺自体が属する点とで交点を持つことは無いとして、AとBとCに属する辺を1つずつ調べていけば良いと思うけど。DとEのどちらにも属してない辺は無いんで、これ自体は難しく無いだろう。
三角形自体は自ずと面というかクラスタなんで、四角形の中に耐震構造のバッテンみたいに三角形を4つ見い出せば(いや四角錐じゃなくて、底辺を共有する三角形を、更に底辺がバッテンになるように重ねたような)、それは流石にクラスタと言えると思うが。
面で無く、平面という概念を導入したとして、グラフで繋がっていれば内角が合計360°、と言えるわけでは無いと思うんだよな。辺が重なるように置くことはできるわけだし。
交点が発生しない(発生するか分からない)ので、結果新しい三角形は無し。新しい三角形が発生しないので、この作図はこのステップでは意味が無かった。
graph := [
A : [
[[B, E], []],
[[D], []]
]
,
B : [
[[A], [E]],
[[C], []]
]
,
C : [
[[B], []],
[[D], []]
]
,
D : [
[[A], []],
[[C], []],
[[E], []]
]
,
E : [
[[A, B], []],
[[D], []]
]
];
triangle_lst := [
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, DA]]
];
always {
ABC_p == 168;
BCD_p == 108;
AB == BC == CD;
ABC_p + ABC_n == 360;
BCD_p + BCD_n == 360;
BAD_p + BAD_n == 360;
ADC_p + ADC_n == 360;
AB == BE;
CBE_p + ABE_h == ABC_n;
ABE_h == 180;
CBE_p + CBE_n == 360;
CBE_p + ABC_p == ABE_h;
ABE_h + ABC_p == CBE_n;
}
次は「点と点の分だけ線を延長」なんだが、1ステップ目のBEが絡んで欲しいんで、CDをC側に延長してみる。新しい点はF。
って、これも交点分からないじゃん。スルー。
じゃあその次は、「2点と、その間の垂直線とどこか1辺の交点による、二等辺三角形の作図」。当然、二等分する辺はBE。
ABやBCは、一旦CEとかを作図して三角形にして、底辺の角度を見て判断すれば良い。そういうのはもうやったことがあると思う。
問題は、CDやADと交わるかどうかの判断。これはBECDとかでクラスタを作らないと、分からないのではないか。
理想としては、辺BCを共有した三角形BCEとBCD、辺DEを共有したCDEとBDE。前者のセットで共有していないDとEの角が、後者のセットのDやEの角の和になっていて、後者のセットで共有していないCとBの角が、前者のセットのCやBの角の和になっている。そうなると流石にそれは面なのではないか。
ちょうど三角形もできるしな。じゃあBECDの全部の点を結んで、うーん、どうしようかな。そういう作図は既にあるんだけど、4ステップ後になってしまう。そもそも、例えばBEとBEの垂直二等分線とADの交点で二等辺三角形を作って、何なんだ?例え導入するにしても、そういうのが必要な問題が出てきてからで良くないか。それなら、BやEに登録してある辺だけ調べれば良くなるわけだし。そうしようか。
だとしたら、Aは無いとして、EとCを結ぶことになるだろうな。
いやでも、このCEの作図がもったいないというか、例えばBCと交わらないと分かったら、CEと交わると分かるわけだし。これは待つのもありなんじゃないかなあ、1ステップだし。
だとしたら、cluster_lstを調べていって、その辺だけ調べていけば良いんじゃないかなあ。具体的にどういう風に手順を組み立てるかは分からないけど、そういう方針で行くという話で。BE関係無いし。
次は、「ある1辺と同じ長さの辺を別の辺に落とすことによる二等辺三角形の作図」。BEをBCに落とすことにする。
俺は見落としていたのだけど、これは落とす方の辺が長かったら、垂線を落とせない可能性があるのだな。
だとしたら、この作図も、すでに判明している三角形に限るべきかもしれない。両方の角が90°以下の時に、垂線と底辺の半分への辺を作図して、昨日みたいに条件式にかける。
今日はここまでで良いか。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その17
ジュニア算数オリンピックにおけるユークリッド幾何学の問題の解答の自動化を模索している。まず三角形定理ループを回し、回答できなかったら1ステップの作図を試していって、それらで回答できるか探る。それでも駄目だったら2ステップ、3ステップと増やしていく。交点の確認はこの方法を使う。
06年度トライアル問題 問題9
『図の四角形ABCDはAB=BC=CDで、角B=168度、角C=108度です。角Dの大きさを求めなさい。
 』
』
どうしよう。一旦最初からやろうかな?そっちの方が分かりやすい気がする。まだ自然言語中心で。
作図
以下5種類の作図をしていく。直接作図したもの以外に三角形や、あるいは正四角形や正五角形ができていたら、次の定理ループで角度が明らかになる可能性がある。
- 点と点を結んで線にする
- 点と点の距離の分だけ線を延長
- 2点と、その間の垂直線とどこか1辺の交点による、二等辺三角形の作図
- ある1辺と同じ長さの辺を別の辺に落とすことによる二等辺三角形の作図
- 同じ図形の作図(同じ長さの辺の所に)
- 正四角形
- 正五角形
じゃあ一番最初の状態を。
graph := [
"A" : [
[["B"], []],
[["D"], []]
]
,
"B" : [
[["A"], []],
[["C"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A"], []],
[["C"], []]
]
];
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
triangle_lst := [
];
cluster_lst := [
["BAD_p", "ABC_p", "BCD_p", "ADC_p"] #ネガティブ同士でもクラスターだと考えるか?いや無いな、辺を追加した時に意味不明になる。
];これは三角形定理ループを回しても、答えには行き着かないんだった。
じゃあまず、1ステップ目のAとCを繋ぐ作図をやってみる。
まずgraphでAとCを繋ぐ。更に2次元の問題なので、繋ぐだけで無く、既存の角を割る動作でもあるはずだ。
点Aだと、BADのポジティブかネガティブを割り、更に新しくBAC・DACのポジティブ・ネガティブが発生しなければいけない。
cluster_lstを見ると、点Aと点Cが登録してあるクラスタがあり(下を参照)、点AとCは結ばれておらず、しかもクラスタのどの角もポジティブなので、点AとCはクラスターの内部で結ばれると分かる。つまり、割られるのはBADのポジティブ側だと分かる。しかも、割られるのがポジティブ側なら、割った後もポジティブ側だと分かる。
"BAC_p" + "DAC_p" == "BAD_p";
"BAC_p" + "BAC_n" == 360;
"DAC_p" + "DAC_n" == 360;
逆側でも同じだ。
"BCA_p" + "DCA_p" == "BCD_p";
"BCA_p" + "BCA_n" == 360;
"DCA_p" + "DCA_n" == 360;
更に、triangle_lstも、点と繋がっている点が更に別の繋がっている点とも繋がっているかを探していくことで、更新することができるだろう。
ポジティブかネガティブかだが、三角形ならまずポジティブだろう。
triangle_lst := [
"△ABC" : ["BAC_p", "AB", "ABC_p", "BC", "BCA_p", "CA"], #命名のルール、どうしようかなあ
"△ADC" : ["DAC_p", "AD", "ADC_p", "DC", "DCA_p", "CA"]
];
図を見て、取得したい情報が取得できているようなので、これで良いということだろう。
graph := [
"A" : [
[["B"], []],
[["D"], []],
[["C"], []]
]
,
"B" : [
[["A"], []],
[["C"], []]
]
,
"C" : [
[["B"], []],
[["D"], []],
[["A"], []]
]
,
"D" : [
[["A"], []],
[["C"], []]
]
];
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
"BAC_p" + "DAC_p" == "BAD_p";
"BAC_p" + "BAC_n" == 360;
"DAC_p" + "DAC_n" == 360;
"BCA_p" + "DCA_p" == "BCD_p";
"BCA_p" + "BCA_n" == 360;
"DCA_p" + "DCA_n" == 360;
triangle_lst := [
"△ABC" : ["BAC_p", "AB", "ABC_p", "BC", "BCA_p", "CA"], #命名のルール、どうしようかなあ
"△ADC" : ["DAC_p", "AD", "ADC_p", "DC", "DCA_p", "CA"]
];
cluster_lst := [
[["A", "B", "C", "D"], ["BAD_p", "ABC_p", "BCD_p", "ADC_p"]] #ネガティブ同士でもクラスターだと考えるか?いや無いな、辺を追加した時に意味不明になる。
];
BとDを繋ぐ処理も、似たような感じになるだろうから、飛ばす。
次はAとBの辺をその分だけ延長してみる。今回はA側に延長しよう。
もちろんその前に、AとBを繋いだ処理を戻す。それはあの記述法の「記録1」だとかを使えば良いだろう。ここでは省略するが。
まず、graphを更新する。追加する点はEとしよう。
すでにあるBADのネガティブかポジティブを割って、更にBAE・DAEのポジティブ・ネガティブを追加しなければいけない。
今回は、Bがクラスタで、そのクラスタの角はどれもポジティブなので、その場合は必ずネガティブを割ることになるんじゃないかな。
しかも、BAEは180°だな。そうすると、もう一方も必ずポジティブになるな。
"BAE_p" + "DAE_p" == "BAD_n";
"DAE_p" + "DAE_n" == 360;
"BAE_p" == 180;
定義も追加する必要があるな。
"AB" == "AE";
図を見ると、"BAD_p" + "DAE_p" == "BAE_p"、である必要もあるな。しかも、"BAD_p" + "BAE_p" == "DAE_n"、である必要もあるのか。
手元で簡単に、1点から3辺が伸びている図を描いてみると、そういうのが3種類発生するはずだから、これで良いのか。
"BAD_p" + "DAE_p" == "BAE_p";
"BAD_p" + "BAE_p" == "DAE_n";
これは保留だけども、"BAE_n"も追加した方が良いのかなあ。そうすると分かりやすくなる気もするけど。
どういう風な流れで捉えたら良いんだろう。3辺だったらこういうのが3種類発生するのは分かったけど。まあ、いいか。
まあとにかく、既存の角を分割して、新しい角のポジティブネガティブ追加して、3辺だったらこういうのが発生して、という。図を見る限りでは、必要な作業はこれだけだな。
graph := [
"A" : [
[["B"], []],
[["D"], []],
[["E"], []]
]
,
"B" : [
[["A"], []],
[["C"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A"], []],
[["C"], []]
]
];
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"BAE_p" == 180;
"AB" == "AE";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
"BAE_p" + "DAE_p" == "BAD_n";
"DAE_p" + "DAE_n" == 360;
"BAD_p" + "DAE_p" == "BAE_p";
"BAD_p" + "BAE_p" == "DAE_n";
triangle_lst := [
];
cluster_lst := [
["BAD_p", "ABC_p", "BCD_p", "ADC_p"] #ネガティブ同士でもクラスターだと考えるか?いや無いな、辺を追加した時に意味不明になる。
];
他の延長も同じだろうから、飛ばす。
じゃあ最初の状態に戻して。次は、垂直二等分線による二等辺三角形の作図。ABを二等分することにしよう。
どの辺に交わるかだけど、今回のクラスタのどれかということなら、ACを作図して角BACと角ABCを比較して、BACの方が大きかったらBCに交わる。BDを作図して角ABDと角BADを比較して、ABDの方が大きかったらADに交わる。そのどちらでも無ければCDに交わる。
graphでACを作成して(クラスタ内なのでポジティブを分割して、それぞれの360°も登録する)、三角形定理ループ(triangle_theorem_loop)を回せば、どちらが大きいかは出るだろう。(その作図を戻すべきかは分からない。とりあえず戻すことにしてみるか。)
BDでも同じ。で、ADに交わると出るかどうか。考えたけど、出るな、△BCDが二等辺三角形で、ABDは132°になる。プログラムとして具体的に考えるなら、「if "ABD_p" > "BAD_p" {~~~} elif ~~~」という具合か。「"BAD_p" + "ADB_p" + 132 == 180」から、「"BAD_p" < 48」を出せれば良いが。
じゃあそういうわけで、ADに点Eを加えて、点Eと点Bを結ぶ。graphをそういう風に更新する(下を参照)。
更に、ADもBも同じクラスタなので、「"ABE_p" + "CBE_p" == "ABC_p"」、「"ABE_p" + "ABE_n" == 360」、「"CBE_p" + "CBE_n" == 360」。
「"AEB_p" + "DEB_p" == "AED_p"」、「"AEB_p" + "AEB_n" == 360」、「"DEB_p" + "DEB_n" == 360」、「"AED_p" == 180」。
定義を追加する。「"AE" == "BE"」。
クラスタを分割したので、cluster_lstに「["B", "C", "D", "E"], ["CBE_p", "BCD_p", "CDE_p", "BED_p"]」も欲しい。A以外で作成すれば良いだろう。
あとはtriangle_lstも更新が必要だろうな。
図を見る限りでは、こんなものだろうか。
graph := [
"A" : [
[["B"], []],
[["D", "E"], []]
]
,
"B" : [
[["A"], []],
[["C"], []],
[["E"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A", "E"], []],
[["C"], []]
]
,
"E" : [
[["A"], ["D"]],
[["B"], []]
]
];
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"AED_p" == 180;
"AE" == "BE";
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
"ABE_p" + "CBE_p" == "ABC_p";
"ABE_p" + "ABE_n" == 360;
"CBE_p" + "CBE_n" == 360;
"AEB_p" + "DEB_p" == "AED_p";
"AEB_p" + "AEB_n" == 360;
"DEB_p" + "DEB_n" == 360;
triangle_lst := [
"△ABE" : ["BAE", "AB", "ABE", "BE", "AEB", "EA"]
];
cluster_lst := [
[("A", "B", "C", "D"), ["BAD_p", "ABC_p", "BCD_p", "ADC_p"]], #今気付いたが、これは[0]はリストじゃなくて順番が無いから集合だな
[("B", "C", "D", "E"), ["CBE_p", "BCD_p", "CDE_p", "BED_p"]]
];
ADなどでも、特に変わる所は無いだろう。同じ長さの辺を繋がっている辺に落とす、に移る。
じゃあ処理したものを元に戻す。
ABと同じ長さの辺を、BCやADに落とす場合を考えてみる。
まずBCは、角ABCが168°なので、90°以上なので無理だ(参照)。
問題はADだが、まずBからADに垂線を垂らす。具体的には、AD上に点Eを作図して、Bと繋げ、角AEB == 90にする。BもADもクラスタ内なので、処理は前にも見たような感じで。
で、AEとAD/2を比較して、もしAD/2の方が大きければ第2条件はクリア(第1条件は後から)。
更にはAD/2(点Fと名付けよう)と点Bを結んで、BAFとBAEを比較する。BAFの方が大きければ第2条件はクリア。
で、第1条件は角BADが90°以下であることだが、今までの作図を使った方が良いので、こちらを後に持ってくる。今までの作図で確認できなければ、辺AD上の点と、点Bを片っ端から繋げて、何とか確認するべきなのかもしれない。本当は辺BDを繋げれば、角BADは90°以下だと確認できるんだが。
ADの第2条件のBEとBFの作図を具体的にやってみようか。
まず点Eから。上に書いたのを反映する。
ただ一点、点Bにおける3辺の角の和が、ABC_pを割るものだから、例えば"CBE_p" + "ABC_n" == "ABE_n"。その判断をどうするかは分からないけど。
次に点F。大体点Eと同じだろう。
BEと交点は発生し得ないんだが、AD上でのEとの関係が問題にはなる。まあそこも問うているわけだが。あと、角の和やクラスタもより複雑になるか(いやクラスタは同じだった)。
ABE_pとCBE_pのどちらを割っているかが問題だな。もっと言えば、分からない状態でどうするか、そして分かった段階でどう反映するか、だとかが問題だな。
暫定解としては、pやnでは無く、1や2と名付ける、だったか。試してみる。いや、駄目だった。
ABF_? + EBF_p == ABE_?
CBF_? + EBF_p ==CBE_?
新しく区切られた方はどっちもポジティブ。もう片方は必ずどっちもネガティブ(もしクラスタの角がポジティブだったらだけど)。
問題は、ABEやCBEにはもうポジティブやネガティブがあることだ。あの記述法のalwaysで、条件式でポジティブやネガティブを入れるか。というより、制約は本質的にalwaysの所に入れるべきなのかな、その時限りでは無いわけだし。そうなるとあの記述法の意味論の問題になってくるわけだが。いや、うん、やはり制約はalwaysの所に入れるべきだな。
1つの点に4辺ある時、角の和は、隣り合う1+1が4種類、(2)+1が8種類、(3)+1が4種類。1+1+1は、三角形で無く角の和だし、いらないんじゃないかなあ。(3)+1は360°で4種類でもう登録してある。3辺の時は、4辺の時を基準にすると、1+1が1種類、(2)+1が2種類登録してあるわけだ。また、Fの時もEを無視するように同じように1種類と2種類が登録してある。更に、割った時にも割った側の1+1と割ってない側の(2)+1が1種類ずつが登録と。
つまり1+1はEBF_p + 割ってない側 == 割ってない側の点とBとF。
(2)+1は、割ってない側の点とBとFのネガティブ + 割ってない側の角 == EBF_n。割ってない側の点とBとFのネガティブ + EBF_p == 割ってない側の角のネガティブ。割った側の角のネガティブ + 割った側のEBFじゃない方 == EBF_n。割った側の角のネガティブ + EBF_p == 割った側のEBFじゃない方のネガティブ。つまり、EBFについての足し算というか、EBF_nについての2種類と、EBF_pについての2種類かな。
条件は、ABEとABFを比較して、小さいほうが大きい方を割っている。あるいはAEとAFを比較して、小さい方が大きい方を割っている。
if "ABE_p" < "ABF_p" or "AE" < "AF" {
"ABF_n" + "EBF_p" == "ABE_n";
"CBF_p" + "EBF_p" == "CBE_p";
"ABF_n" + "ABE_p" == "EBF_n";
"CBE_n" + "CBF_p" == "EBF_n";
"ABF_n" + "EBF_p" == "ABE_n";
"CBE_n" + "EBF_p" == "CBF_n";
} elif "ABE_p" > "ABF_p" or "AE" > "AF" {
"ABF_p" + "EBF_p" == "ABE_p";
"CBF_n" + "EBF_p" == "CBE_n";
"ABE_n" + "ABF_p" == "EBF_n";
"CBF_n" + "CBE_p" == "EBF_n";
"ABE_n" + "EBF_p" == "ABF_n";
"CBF_n" + "EBF_p" == "CBE_n";
} elif "ABE_p" == "ABF_p" or "AE" == "AF" {
graphの"E"と"F"を統合(今回は"F"を消す)。
"F"が入る三角形とクラスタを消す。
alwaysの式の"F"を"E"に書き換えた上で、被ったものを消す。
この条件式自体を消す。
}
いや、違うな。条件("AE" < "AF"とか)を満たしたら、BADが90°以下かを確認するのか。それ以外の条件を満たした場合は、だからこの作図は無意味で、元に戻して根本的に次の作図に取りかかれば良いのか。
("AE" < "AF")とかに限って、そのままBADが90°以下かの確認に進むかな?しかし、本当に順番はこれで良いのかな。EやFは作図して終わりだと思ってたから、こういう条件による分岐が入ってくると話が違ってきてるんだよな。
人間だったらどうするのかな。点BからAD上の点全部に作図したら話は早いけどね。でも後から戻すとはいえ、その作図は並行した同じステップでやっているわけで、この確認は次のステップに回した方が計算量は少ない気もする。
そうしようかな。だから、条件式前の下の段階で、("AE" < "AF")とかの条件にかけて、当てはまったら作図を元に戻して、点BからAD上へABと同じ長さの辺を作図するということにしようか。
graph := [
"A" : [
[["B"], []],
[["D", "E", "F"], []]
]
,
"B" : [
[["A"], []],
[["C"], []],
[["E"], []],
[["F"], []]
]
,
"C" : [
[["B"], []],
[["D"], []]
]
,
"D" : [
[["A", "E", "F"], []],
[["C"], []]
]
,
"E" : [
[["A"], ["D"]],
[["B"], []],
[["F"], []]
]
,
"F" : [
[["A"], ["D"]],
[["B"], []],
[["E"], []]
]
];
triangle_lst := [
"△ABE" : ["BAE_p", "AB", "ABE_p", "BE", "AEB_p", "EB"],
"△ABF" : ["BAE_p", "AB", "ABF_p", "BF", "AFB_p", "FB"],
"△BEF" : ["EBF_p", "BE", "BEF_p", "EF", "BFE_p", "FB"]
];
cluster_lst := [
[("A", "B", "C", "D"), ["BAD_p", "ABC_p", "BCD_p", "ADC_p"]],
[("B", "C", "D", "E"), ["CBE_p", "BCD_p", "CDE_p", "BED_p"]],
[(""B", "C", "D", "F"), ["CBF_p", "BCD_p", "CDE_p", "BFD_p"]]
];
always {
"ABC_p" == 168;
"BCD_p" == 108;
"AB" == "BC" == "CD";
"AEB_p" == 90;
"AED_p" == 180;
"AF" == "DF";
"AFD_p" == 180;
"ABC_p" + "ABC_n" == 360;
"BCD_p" + "BCD_n" == 360;
"BAD_p" + "BAD_n" == 360;
"ADC_p" + "ADC_n" == 360;
"ABE_p" + "CBE_p" == "ABC_p";
"ABE_p" + "ABE_n" == 360;
"CBE_p" + "CBE_n" == 360;
"AEB_p" + "BED_p" == "AED_p";
"AEB_p" + "AEB_n" == 360;
"BED_p" + "BED_n" == 360;
"BED_p" + "AED_p" == "AEB_n";
"AEB_p" + "AED_p" == "BED_n";
"CBE_p" + "ABC_n" == "ABE_n";
"ABE_p" + "ABC_n" == "CBE_n";
"ABF_p" + "CBF_p" == "ABC_p";
"ABF_p" + "ABF_n" == 360;
"CBF_p" + "CBF_n" == 360;
"AFB_p" + "BFD_p" == "AFD_p";
"AFB_p" + "AFB_n" == 360;
"BFD_p" + "BFD_n" == 360;
"BFD_p" + "AFD_p" == "AFB_n";
"AFB_p" + "AFD_p" == "BFD_n";
"CBF_p" + "ABC_n" == "ABF_n";
"ABF_p" + "ABC_n" == "CBF_n";
}
他の辺も、同じようにできるだろう。
次は、同じ長さの辺の上に、同じ図形を作図する。
ただ、三次元で思い描いた時に、例えばADを重ねるにしても、それを軸に回転できるというか、かなり自由にできることが分かる。
この問題以降の問題も見てみて考えるに、これはクラスタとクラスタを合わせてクラスタを拡大するということじゃないかと思うので、暫定的にそういうことにする。
そうすると、四角形だけじゃなく三角形も、五角形も、何角形だろうが、クラスタとして扱わなければならないのではないか。
そして、クラスタを同じ方向に重ね合わせて、交点を確認するというのは、不毛なのではないか。
だとしたら、絶対に三角形が発生することは無いので、1ステップでは無駄だ。しかし、試しにそのクラスタの拡大だけはやってみよう。
ABとBCを重ねてみよう。元CをE、元DをFとする。
[["B", "C", "E", "F"], ["CBF_p", "BC", "BCE_p", "CE", "CEF_p", "EF", "BFE_p", "FB"]]
"BCE_p" == 168;
"CEF_p" == 108;
"BC" == "CE" == "EF";
"BCE_p" + "BCE_n" == 360;
"CEF_p" + "CEF_n" == 360;
"CBF_p" + "CBF_n" == 360;
"BFE_p" + "BFE_n" == 360;
で、こうしたい。
[["A", "B", "F", "E", "C", "D"], ["BAD_p", "AB", "ABF_?", "BF", "BFE_p", "EF", "CEF_p", "CE", "DCE_?", "CD", "ADC_p", "AD"]
ABC_p + CBF_p == ABF_?
BCD_p + BCE_p == DCE_?
["A", "B", "C", "D"]と["B", "C", "E", "F"]だが、後者は["C", "E", "F", "B"]でもあって、これをひっくり返すと["B", "F", "E", "C"]。それをそのまま挿入してこの結果になる。つなぎ目のBとCの角は、足し算で記述する必要がある、がポジティブかネガティブかが確実に分かるわけでは無い。
EとFは新しい点なので、今度こそ「ABF_1」とかで良いのかもしれない。
…そもそも、クラスタで考えず「ABC_p + CBF_p == ABF_1」じゃ駄目なのかな。3Dでそのルールを守りながら違う図を描けるから駄目なのか。
で、alwaysでif文を作って、満たし次第その条件文は消去することにするか。
このクラスタ、面なんじゃないかな。
ユークリッド幾何学以外における記述法と三角形定理ループの統合
元の記述法と統合することになったんで、まずは三角形定理ループだとかを元の記述法に置き換えてみた。
triangle_lst = [
"△ABC" : ["HAI", "AB", "CBI", "BC", "BCH", "AC"],
"△ACD" : ["DAH", "AC", "DCH", "CD", "ADC", "AD"],
"△ADH" : ["DAH", "AD", "ADG", "DH", "AHG", "AH"],
"△ADI" : ["DAI", "AD", "ADG", "DI", "AIH", "AI"],
"△AHI" : ["HAI", "AH", "AHI", "HI", "AIH", "AI"],
"△BEI" : ["EBI", "BE", "BEI", "EI", "BIE", "BI"],
"△CDE" : ["BCD", "CD", "CDG", "DE", "BEI", "CE"],
"△CDG" : ["DCG", "CD", "CDG", "DG", "CGD", "CG"],
"△CDH" : ["DCH", "CD", "CDG", "DH", "CHG", "CH"],
"△CEF" : ["BCF", "CE", "BEF", "EF", "CFE", "CF"],
"△CEG" : ["BCG", "CE", "BEI", "EG", "CGH", "CG"],
"△CEH" : ["BCH", "CE", "BEI", "EH", "CHI", "CH"],
"△CGH" : ["GCH", "CG", "CGH", "GH", "CHG", "CH"],
];
"AD" == "BC" == "EG" == "CF";
"AB" == "CD" == "EF" == "CG";
"DAI" == "BCD" == "FEI" == "EBI" == "CGD";
"ADC" == "CBI" == "CFE" == "CGH";
"AHG" == "CHI";
"AHI" == "CHG" == "FCH";
"AIH" == "BIE" == "CGG";
"AIE" == "BIH";
"DAH" == "BCH";
"ADG" == "BEI" == "BCF";
"HAI" == "DCH";
"BEF" == "BCG";
"DAH" + "HAI" == "DAI";
"EBI" + "CBI" == 180;
"DCG" + "GCH" == "DCH";
"GCH" + "BCH" == "BCG";
"BCH" + "BCF" == "FCH";
"DCH" + "BCH" == "BCD";
"BCG" + "DCG" == "BCD";
"BCG" + "BCF" == "FCG";
"FCH" + "GCH" == "FCG";
"BCD" + "BCF" == "DCF";
"FCG" + "DCG" == "DCF";
"ADG" + "CDG" == "ADC";
"BEI" + "BEF" == "FEI";
"CGD" + "CGH" == 180;
"AHG" + "CHG" == 180;
"AIH" + "AIE" == 180;
"HAI" + "BCH" == "EBI";
"BCG" + "BEI" == "CGD";
"DAH" + "ADG" == "AHI";
"DAI" + "ADG" == "AIE";
"DCG" + "CDG" == "CGH";
"EBI" + "BEI" == "BIH";
"BEI" + "BIE" == "CBI";
"HAI" + "AHI" == "BIH";
"HAI" + "AIH" == "AHG";
"DCH" + "CDG" == "AHG";
"GCH" + "CGH" == "CHI";
"GCH" + "CHG" == "CGD";
"AI" + "BI" == "AB";
"AH" + "CH" == "AC";
"BC" + "BE" == "CE";
"DG" + "EG" == "DE";
"DH" + "EH" == "DE";
"DI" + "EI" == "DE";
"DG" + "GH" == "DH";
"DG" + "GI" == "DI";
"DH" + "HI" == "DI";
"EI" + "GI" == "EG";
"EH" + "GH" == "EG";
"EI" + "HI" == "EH";
"GH" + "HI" == "GI";
def ele1_equal_ele2(ele1, ele2, loop_flg, exe_flg) {
if not (ele1 == ele2) {
ele1 == ele2;
loop_flg := True;
exe_flg := True;
}
return loop_flg, exe_flg;
}
def isosceles_angle_check(triangle_lst, exe_flg) {
loop_flg := True;
while loop_flg {
loop_flg := False;
for tri1 in triangle_lst.values() {
for angle1, angle2, side1, side2 in [(tri1[0], tri1[2], tri1[5], tri1[3]), (tri1[2], tri1[4], tri1[1], tri1[5]), (tri1[0], tri1[4], tri1[1], tri1[3])] {
if angle_1 == angle_2 {
loop_flg, exe_flg := ele1_equal_ele2(side1, side2, loop_flg, exe_flg);
}
}
}
}
return triangle_lst, exe_flg;
}
def isosceles_side_check(triangle_lst, exe_flg) {
loop_flg := True;
while loop_flg {
loop_flg := False;
for tri1 in triangle_lst.values() {
for side1, side2, angle1, angle2 in [(tri1[1], tri1[3], tri1[0], tri1[4]), (tri1[3], tri1[5], tri1[2], tri1[0]), (tri1[1], tri1[5], tri1[2], tri1[4])] {
if side1 == side2 {
loop_flg, exe_flg := ele1_equal_ele2(angle1, angle2, loop_flg, exe_flg);
}
}
}
}
return triangle_lst, exe_flg;
}
def two_angle_check(triangle_lst, exe_flg) {
loop_flg := True;
while loop_flg {
loop_flg := False;
for tri1 in triangle_lst.values() {
for tri2 in triangle_lst.values() {
if tri1 == tri2 {
continue;
}
for angle_1_A, angle_1_B in itertools.combinations([tri1[0], tri1[2], tri1[4]], 2) {
for angle_2_A, angle_2_B in itertools.combinations([tri2[0], tri2[2], tri2[4]], 2) {
if (angle_1_A, angle_1_B) == (angle_2_A, angle_2_B) {
angle_1_C := [A for A in [tri1[0], tri1[2], tri1[4]] if A not in [angle_1_A, angle_1_B]][0];
angle_2_C := [A for A in [tri2[0], tri2[2], tri2[4]] if A not in [angle_2_A, angle_2_B]][0];
loop_flg, exe_flg := ele1_equal_ele2(angle_1_C, angle_2_C, loop_flg, exe_flg);
}
}
}
}
}
}
return triangle_lst, exe_flg;
}
def angle_side_angle(triangle_lst, exe_flg) {
loop_flg := True;
while loop_flg {
loop_flg := False;
for tri1 in triangle_lst.values() {
for tri2 in triangle_lst.values() {
if tri1 == tri2 {
continue;
}
for angle_1_A, side_1, angle_1_B, side_1_X, angle_1_C, side_1_Y in [(tri1[0], tri1[1], tri1[2], tri1[3], tri1[4], tri1[5]), \
(tri1[2], tri1[3], tri1[4], tri1[5], tri1[0], tri1[1]), \
(tri1[4], tri1[5], tri1[0], tri1[1], tri1[2], tri1[3])] {
for angle_2_A, side_2, angle_2_B, side_2_X, angle_2_C, side_2_Y in [(tri2[0], tri2[1], tri2[2], tri2[3], tri2[4], tri2[5]), \
(tri2[2], tri2[3], tri2[4], tri2[5], tri2[0], tri2[1]), \
(tri2[4], tri2[5], tri2[0], tri2[1], tri2[2], tri2[3])] {
if side_1 == side_2 && (angle_1_A, angle_1_B) == (angle_2_A, angle_2_B) {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_C, angle_2_C, loop_flg, exe_flg);
if angle_1_A == angle_2_A {
loop_flg, exe_flg := ele1_equal_ele2(side_1_X, side_2_X, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(side_1_Y, side_2_Y, loop_flg, exe_flg);
} else {
loop_flg, exe_flg := ele1_equal_ele2(side_1_X, side_2_Y, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(side_1_Y, side_2_X, loop_flg, exe_flg);
}
}
}
}
}
}
}
return triangle_lst, exe_flg;
}
def side_angle_side(triangle_lst, exe_flg) {
loop_flg := True;
while loop_flg {
loop_flg := False;
for tri1 in triangle_lst.values() {
for tri2 in triangle_lst.values() {
if tri1 == tri2 {
continue;
}
for side_1_A, angle_1, side_1_B, angle_1_X, side_1_C, angle_1_Y in [(tri1[1], tri1[2], tri1[3], tri1[4], tri1[5], tri1[0]), \
(tri1[3], tri1[4], tri1[5], tri1[0], tri1[1], tri1[2]), \
(tri1[5], tri1[0], tri1[1], tri1[2], tri1[3], tri1[4])] {
for side_2_A, angle_2, side_2_B, angle_2_X, side_2_C, angle_2_Y in [(tri2[1], tri2[2], tri2[3], tri2[4], tri2[5], tri2[0]), \
(tri2[3], tri2[4], tri2[5], tri2[0], tri2[1], tri2[2]), \
(tri2[5], tri2[0], tri2[1], tri2[2], tri2[3], tri2[4])] {
if angle_1 == angle_2 and (side_1_A, side_1_B) == (side_2_A, side_2_B) {
loop_flg, exe_flg := ele1_equal_ele2(side_1_C, side_2_C, loop_flg, exe_flg);
if side_1_A == side_2_A {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_X, angle_2_X, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_Y, angle_2_Y, loop_flg, exe_flg);
} else {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_X, angle_2_Y, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_Y, angle_2_X, loop_flg, exe_flg);
}
}
}
}
}
}
}
return triangle_lst, exe_flg;
}
def side_side_side(triangle_lst, exe_flg) {
loop_flg := True;
while loop_flg {
loop_flg := False;
for tri1 in triangle_lst.values() {
for tri2 in triangle_lst.values() {
if tri1 == tri2 {
continue;
}
angle_1_A, side_1_A, angle_1_B, side_1_B, angle_1_C, side_1_C := tri1;
angle_2_A, side_2_A, angle_2_B, side_2_B, angle_2_C, side_2_C := tri2;
if (side_1_A, side_1_B, side_1_C) == (side_2_A, side_2_B, side_2_C) {
if side_1_A == side_2_A {
if side_1_B == side_2_B {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_A, angle_2_A, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_B, angle_2_B, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_C, angle_2_C, loop_flg, exe_flg);
} elif side_1_B == side_2_C {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_A, angle_2_B, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_B, angle_2_A, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_C, angle_2_C, loop_flg, exe_flg);
}
} elif side_1_A == side_2_B {
if side_1_B == side_2_A {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_A, angle_2_C, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_B, angle_2_B, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_C, angle_2_A, loop_flg, exe_flg);
} elif side_1_B == side_2_C {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_A, angle_2_B, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_B, angle_2_C, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_C, angle_2_A, loop_flg, exe_flg);
}
} elif side_1_A == side_2_C {
if side_1_B == side_2_A {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_A, angle_2_C, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_B, angle_2_A, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_C, angle_2_B, loop_flg, exe_flg);
} elif side_1_B == side_2_B {
loop_flg, exe_flg := ele1_equal_ele2(angle_1_A, angle_2_A, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_B, angle_2_C, loop_flg, exe_flg);
loop_flg, exe_flg := ele1_equal_ele2(angle_1_C, angle_2_B, loop_flg, exe_flg);
}
}
}
}
}
}
return triangle_lst, exe_flg;
}
def triangle_theorem_loop(triangle_lst) {
exe_flg := True;
while exe_flg:
exe_flg := False;
triangle_lst, exe_flg := isosceles_angle_check(triangle_lst, exe_flg);
triangle_lst, exe_flg := isosceles_side_check(triangle_lst, exe_flg);
triangle_lst, exe_flg := two_angle_check(triangle_lst, exe_flg);
triangle_lst, exe_flg := angle_side_angle(triangle_lst, exe_flg);
triangle_lst, exe_flg := side_angle_side(triangle_lst, exe_flg);
triangle_lst, exe_flg := side_side_side(triangle_lst, exe_flg);
return triangle_lst;
}
triangle_lst := triangle_theorem_loop(triangle_lst);