ジュニア算数オリンピック 二次元上の面積を求める幾何の問題 「完全に格子」1
このページの問題を、基本的には上から解いていこうかと思っている。
99年度トライアル問題 問題4
『4つの同じ大きさの長方形で図のように大きな正方形をつくるとまん中にも小さな正方形ができます。大きな正方形の面積が49cm^2、まん中の小さな正方形の面積が16cm^2です。
長方形の短い辺の長さは何cmですか。
 』
』
(a + b)^2 == 49
(a - b)^2 == 16
という式を立てるだけなんだが。
a + b == 7
a - b == 4
a + a == 11
a == 5.5
b == 1.5
で答えは1.5だろうか。
99年度トライアル問題 問題14
『たて11cm、よこ17cmの長方形の中に同じ形で同じ大きさの小さな長方形を4つ、A(図1)、B(図2)のように2通りの方法で入れました。斜めの線の部分の周囲の長さはAとBではどちらがどれだけ長いですか。
 』
』
短い方の辺をx、長い方の辺をyとする。
すると、「(x * 2) * 2 + (11 - y) * 2」と「y * 2 + (11 - x * 2) * 2」ではどちらが大きいかを問うている。
左の式は展開すると、「x * 4 - y * 2 + 22」。右の式は、結果的に「- x * 4 + y * 2 + 22」になる。
整理すると、「x * 2 - y」と「- x * 2 + y」ではどちらが大きいかを問うている。
最初の図から条件を読み取ろうとするわけだが、「17 > x * 4」、「11 > y」、というのが読み取れるぐらいだろうか。
二番目の図からは、「17 == y + x * 2」(ちなみに「2 * x」の方が慣れ親しみがありそうだから次回からはそうする)、「11 > x * 2」、というのが読み取れるか。
17 > x * 4
11 > y
17 == y + x * 2
11 > x * 2
「17 > x * 4」は、「8.5 > x * 2」でもあるな。より制約が強いそちらを残そう。
8.5 > x * 2
11 > y
17 == y + x * 2
この手の問題は苦手だったからよく分からないけど、「6 < x * 2」というのが言えそうだな。「」。いやちょっと待てよ。
「17 > x * 4」と「17 == y + x * 2」で、「y + x * 2 > x * 4」が言えるじゃないか。とすると、「y > x * 2」が言える。
「x * 2 - y」と「- x * 2 + y」ではどちらが大きいかを問うているわけだから、yの方が大きいなら後者だな。
あ、いや違うな。問題を読み間違えていた。申し訳ない。(まあ本当の本当に自分の研究の実際を、いかにどうとでも転がり得たものだったかを黒歴史として残すために残しているだけだから、真面目に読む方が捉え方として間違えているのだと俺は思うけども。出来上がりはもっと分かりやすくなる、というより、俺の直接的な仕事がというよりデカルト座標のような残り方をしたら、俺としてはそりゃ最高の状態だわな。技法としての洗練は後からの人間が勝手にやる。俺の昔の言語研究と同じで、間違っていてもコンセプトさえ伝わればそれで良い、技法なのだから良い結果が出ればその結果が保証する。コンピューターと圏論の連結は、当たり前のものでありながらなぜか成されていないし、ユークリッド幾何のグラフによる自動解答をここまで論理的に持ってきているのはやっぱり自画自賛になるが凄いと思う、やろうとする所が偉い)
「(x * 4 - y * 2 + 22) + (- x * 4 + y * 2 + 22) == 44」と、図1の斜めである「(x * 4) * 2 + y * 2 + (17 - x * 4) * 2 + (11 - y) * 2」の比較なのか。
図1の方を展開したら、「x * 8 + y * 2 + 34 - x * 8 + 22 - y * 2 == 56」で、以上とか以下とか考えなくても図1の方だったか。
99年度ファイナル問題 問題5
『下の図は正方形ABCDの中に、面積が100cm^2の正方形の紙を3枚(あ)、(い)、(う)の順番に重ねておいたものです。
上から見えている部分の面積はそれぞれ、70cm^2、80cm^2、100cm^2です。(ア)、(イ)の面積をそれぞれ求めなさい。
 』
』
同じようなアプローチで解けるんじゃなかろうか。
辺の長さは、横軸方向には5つに分けられるので、それぞれA、B、C、D、Eと名付ける。縦軸方向には3つに分けられるので、それぞれF、G、Hと名付ける。
そうすると、アは「A * F」。イは「E * F」。「B + C + D == 10」、「F + G == 10」。「A + B + C == 10」、「G + H == 10」。「C + D + E == 10」。「(B + C) * G == 20」。「C * 10 + D * G == 30」。
みたいな感じだろうか。
A == D
B == E
が言えるな。後者を前者に書き換えよう。
アは「A * F」
イは「B * F」
「B + C + A == 10」
「F + G == 10」
「A + B + C == 10」
「G + H == 10」
「C + A + B == 10」
「(B + C) * G == 20」
「C * 10 + A * G == 30」
整理してみる。
アは「A * F」
イは「B * F」
「A + B + C == 10」
「F + G == 10」
「G + H == 10」
「(B + C) * G == 20」
「C * 10 + A * G == 30」
F == H
が言えるな。後者を前者に書き換えよう。
アは「A * F」
イは「B * F」
「A + B + C == 10」
「F + G == 10」
「(B + C) * G == 20」
「C * 10 + A * G == 30」
あー、で見逃してたけど、CとGはイコールだな。
アは「A * F」
イは「B * F」
「A + B + C == 10」
「F + C == 10」
「(B + C) * C == 20」
「C * 10 + A * C == 30」。「(A + 10) * C == 30」。
「C * 10 + A * C == 30」を整理すると「(A + 10) * C == 30」。Cを明らかにしたいんで、「(B + C) * C == 20」を足してみようか。
「(A + 10 + B + C) * C == 50」。更に「A + B + C == 10」と合わせて、「20 * C == 50」。「C == 50 / 20 == 5 / 2」。
AとBとFが残っているわけだが、Aは、「(A + 10) * C == 30」から「A == 2」だと分かる。
Bは、「A + B + C == 10」から、「2 + B + 2.5 == 10」で、5.5だと分かる。
Fは、「F + C == 10」から、7.5だと分かる。
アは「A * F」なので「2 * 7.5 == 15」。イは「B * F」なので「5.5 * 7.5 == 41.25」らしい。本当かよと思ったら合ってた。
01年度トライアル問題 問題1
『下の図は1つの正方形を、形も大きさも同じ3つの長方形に分けたものです。1つの長方形の周りの長さが16cmのとき、正方形の周りの長さは何cmですか。
 』
』
長方形の短い方の辺をa、長い方の辺をbとする。
2 * a + 2 * b == 16
3 * a == b
この二つから
2 * a + 2 * (3 * a) == 16
2 * a + 6 * a == 16
8 * a == 16
a == 2
b == 6
正方形の周りの長さは24だと分かる。
今回は全般的にこんな解き方で良いのかと思うけど、ユークリッド幾何学でも三角形の角からもう一方の辺に伸びている辺が垂線の時に、それらの掛け合わせ / 2になるだけで、やることは変わらないのでこれで良いのだと思う。
ジュニア算数オリンピックの面積が入るユークリッド幾何の問題の再分類
結構ゴミ箱みたいに押し込んでいたんで、問題の種類ごとに再分類してみた。とりあえずは上から解いていく予定。難しいものは後に回す。
「完全に格子」
99トラ4 格子 もう完全に
99トラ14 完全に系
99ファ5 完全に系なんじゃないか、ユークリッドじゃないことは確か
01トラ1
02トラ4
06トラ7 三角形は誤魔化しというか、ユークリッドでは無い気がした
10トラ1
13トラ10
「格子」
97トラ2 格子 輪ゴム
00トラ4
05ファ6 簡単な問題1問と、簡単な他の普通の問題で、無視して良いことが分かった。
「普通」
97ファ2
00トラ9
01トラ2 一見普通じゃないが、あの体系でも詳しく指定する必要は無いので
01ファ5
03ファ4
04トラ5
04ファ2
05トラ8
06ファ7
08トラ5
08ファ7
09ファ4
09ファ7
10トラ7
10ファ4
11トラ9
11ファ4
12トラ10
13ファ5 多分
「円」
98トラ5 円 敷き詰め
98ファ4 円 普通に解けそう
07トラ2 回転って円じゃないか?
「敷き詰め?」
99トラ7 敷き詰め
99トラ8 敷き詰めというか被りというか、元々の図形の組み合わせで
「謎」
02トラ9 台形を折る問題
07ファ6 困った 新しい作図が必要だ 分かっている何かに変換しようという動き
13ファ2 制約が入る 一つ上と同じ但書「cmだが面積では無い?」
算数オリンピック 二次元上のユークリッド幾何の変則的な問題 その2
グラフで表現したユークリッド幾何学の自動解答に挑戦している。
今回は、算数オリンピックにおける、二次元上のユークリッド幾何の面積が出てこない種類の問題における、変則的な問題を取り上げる。今回は円の問題を取り上げる。
94年度トライアル問題 問題7
『ケーキは、ま上から見ると図のような正五角形で、点線の部分にもようが描かれている。
中央の5本の曲線に囲まれた、ななめの線の部分の周囲の長さはどれだけでしょう。
点数はすべてケーキの頂点を中心にして描いた半径12cmの円周の一部、円周率を3.14として計算してね。
 』
』
円の問題だけど、おそらく円を作図することは無くて、その意味では最初から、円の中心から辺を追加しておいて、それぞれの辺の長さをイコールとしておくだけで良い気もする。
この問題で例えると、外側の五角形の頂点を上から反時計回りでA、B、C、D、E、また内側の五角形の頂点を同じようにF、G、H、I、Jとすると、AB == AH == AI == AEという風にするだけで良い気もする。
しかし、この問題は円の長さを答えとして求めているわけで、それでは解けない。その場合には、ちょうど問題を解ける分だけ円をデータ構造で定義する必要があるのかもしれない。
その場合は、
circle_lst := [
[円の中心の点, [その円に属する点を適当に]],
以下同じように続いていく
];という風に定義すれば良いのではないか。弧は、例えば「⌒IAH」という風に記述する。このIAHは時計回りで、ちょうど∠IAHに対応する(なんで反時計回りで点を名付けてしまったんだろう)。
円の中心からそれぞれの点への辺は自動的にイコールで登録され、弧の具体的な長さは例えば今回だと「AI * 2 * 3.14 * ∠IAH \ 360」という風になるだろう。
今回はAIの長さは分かっているので、∠IAHの大きさが問題になる。初期条件で∠EABは、正五角形の一角、108°で登録されているので、そこから正三角形の一角の60°を2個引いて、-12°でなんとか12°だと分かるんじゃないかな、多分。
分かり次第表示するって、どう書くんだっけか?
96年度ファイナル問題 問題5
『円周上に点がいくつかならんでいます。これらの点を一つおきに直線でつないでいったところ、すべての点を通って、はじめの点にもどりました。こうしてできた図形のとがった部分の角度(図の黒い角の部分)の合計は2700度でした。
円周上に点はいくつありますか。
 』
』
これは難しい問題で、決まった状態から別の状態というか値を弾き出すのでは無く、ルールで最初の状態を弾き出さないといけない。
答えを見ると、三角形の頂点じゃない2角は、頂点側から延長した外角と同じで、その外角がちょうど一つ飛ばした先での(への?)方向転換分の角度になっていて、それが2周分なんで720°らしい。
で頂点の合計が2700°なので、2700 + 720 == 3420°を180°で割って、19個。が答えらしい。
作図の手数の問題というより、方向転換分2周で720°、というのが分からん。分からんというのが正直な感想だ。
04年度ファイナル問題 問題3
『図のように全長30cmの直角に曲がったコース上を、円がはしからはしまで離れることもすべることもなく転がりました。円周上の一点をPとし、点Pがコースのはしにふれている状態から転がり始めたところ、転がり終わったときにも、点Pがコースのはしにふれていました。また、転がり始めと転がり終わり以外で、点Pがコースにふれたことはありませんでした。
このとき、円の半径は何cmでしょうか。円周率は3.14として、答えが割り切れない場合は、小数第三位を四捨五入しなさい。また、もし答えが複数ある場合は、それらをすべて書きなさい。
ただし、解答らんのすべてのワクを使うとは限りません。
 』
』
これは転がるという動きがあるので、どちらかというと昔やった連続的な問題という奴なのかと思う。いやある一定のスピードで加算されていくというわけじゃないから、そうでは無いのか。答えを見た。
完全に右の壁に接触するまでは、下の床? - 半径だけ転がる。右の壁を転がる時には、右の壁 - 半径だけ転がる。
もし右の壁に接触した時に、隅っこの「円周/4」の所に点が無いなら、「円周 * 3 / 4 == 下の床の長さ - 半径 + 右の壁の長さ - 半径」。
もし隅っこに点があったなら、「円周 * 7 / 4 == 下の床の長さ - 半径 + 右の壁の長さ - 半径」だろう。
こういうただ式を立てる問題は、ジャンル分けするなら代数学なのかなと思う。
05年度ファイナル問題 問題1
『午後6時30分北の空に北極星Nと直角二等辺三角形の形になる星A、B、Cが図のように見えました(Nの左にB、Bの上にC、Cの左にAで、NB=BC=CA)。
何時間か後に星Aと星Bが同時に地平線に沈みました。そのあと星Cが沈みました。星Cが沈んだ時刻を求めなさい。ただし、星A、B、Cは北極星の周りを24時間かけて反時計回りに1周します。また地平線は水平な直線とします。
 』
』
答えを見た。この問題は難しいな。
解答のプロセスは2段階に分かれていて、まず、ACNBをクラスタと見なして、Nを共有して、また新しい方のAとBが地平線の上にあるようなのを作図する。そうすると、新しい方の角BNCが45°だと分かる。(新しいCNと地平線が平行だとも分かるらしい。)
星は北極星を中心に一時間に15°回転すると書いてあるので、3時間分だと分かる。
新しいCNから、更に新しいCNを平行線上に更に新しいCが来るように作図する。
2番目のCから垂線を下ろすと、(答えの図を見ながら書いているが)二等辺三角形が発生して、2番目のCNの半分の長さだと分かる。
2番目のCN == 更に新しいCN、かつ、2番目のCからの垂線 == Nからの垂線。これで更に新しいCNと、その垂線の比率が明らかになって、なんか直角だと(厳密にはピタゴラスの定理)で比率というか三角形の種類で角度が分かって、頂点側が60°だと分かる。
で、地平線だとかそういうので、2番目のCNと最後のCNの角度は30°だと分かって、2時間進んだと分かる、らしい。
それで答えは5時間。
時間の進みがあって、しかも2段階に分けて答えなきゃいけないのが嫌だったな。2つのACNBを設定して、地平線上にCがある更に新しいCNを設定すれば、色々なCNの角の足し算を答えになるように設定しておけば自動で出たりしたのかな。
分からないな。まあ参考にする感じで見返しにこれば良いと思うけど。
算数オリンピック 二次元上のユークリッド幾何の変則的な問題 その1
グラフで表現したユークリッド幾何学の自動解答に挑戦している。
今回は、算数オリンピックにおける、二次元上のユークリッド幾何の面積が出てこない種類の問題における、変則的な問題を取り上げる。
94年度ファイナル問題 問題4
『図1のような、AとBの二つの三角形があります。それぞれを、図2のように切り分けると、Aからできる二つの三角形と、Bからできる二つの三角形とで、たがいに相似(そうじ)の三角形の組が二組となります。
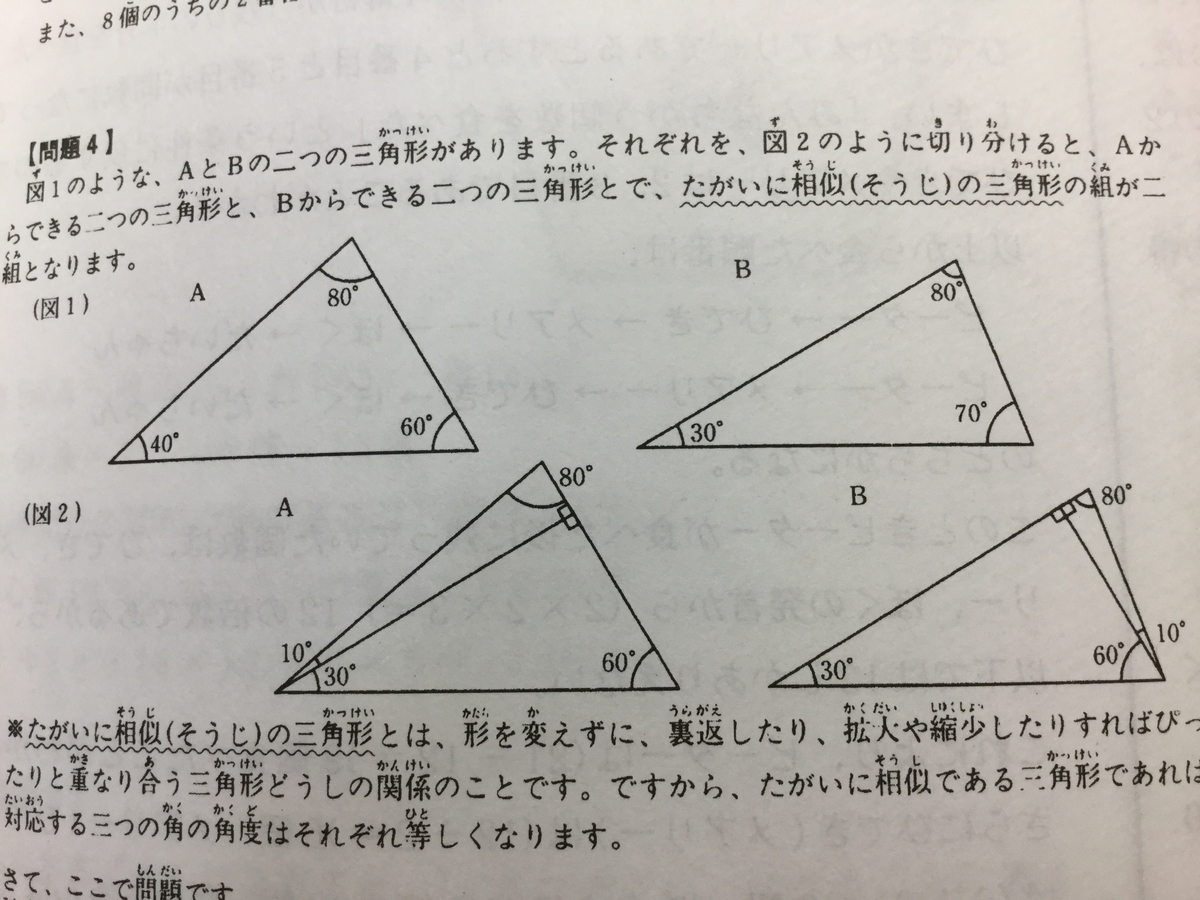
※たがいに相似(そうじ)の三角形とは、形を変えずに、裏返したり、拡大や縮小したりすればぴったりと重なり合う三角形どうしの関係のことです。ですから、たがいに相似である三角形であれば、対応する三つの角の角度はそれぞれ等しくなります。
さて、ここで問題です。
今度は、直角二等辺三角形と正三角形とをそれぞれ三つの三角形に切り分けます。
直角二等辺三角形からできる三つの三角形と、正三角形からできる三つの三角形とで、たがいに相似の三角形の組が三組となるように、切れこみを入れなさい。
また、切り分けてできる三角形のすべての角に、角度を書き入れなさい。』
今までの問題は、角度や辺の値を明らかにせよというものだったが、これは作図がゴールになっている。今までの自分の体系で言えば、クラスタの作図がゴールになっている。
それも、クラスタを分割したら、分割元のクラスタは答えから外さなければいけない。
決められた、それも値を求める問題に無い種類の作図をステップとして定義して、答えに至る。
cluster_lstのリストの数字を登録するリストを定義して、その中の一つをcluster_lstから選び、分割して、その数字自体は消す。
既存の流れから、他の作図を外し、その作図に差し替える。リストの登録もその作図のステップの内に入れて良いだろう。
作図をする際には角度は具体的には決めない方が良いだろう。三角形1つであれば3通りの作図、2つであれば6通りの作図、3つであれば9通りの作図がある。その結果同士で、リストに登録されたクラスタの、角度の集合を用意し、2つの結果のその集合がイコールだという制約を入れて、結果が一つでも出れば打ち止めにする(結果の一つ、という風に命令して、最適化は言語側がやってくれるだろう)。
応用だが、そこまで難しい応用というわけじゃない。こういう問題の数が出揃い次第、自然言語でない記述方法を考えたいと思う。
98年度ファイナル問題 問題6
『ある1つの多角形を何本かの直線で切りはなし、いくつかの多角形に分けました。
すると、分けてできた多角形の辺の数の合計は、もとの多角形の辺の数より13本多く、内角の合計はもとの多角形の内角の和の1.3倍になりました。
もとの多角形は何角形でしたか。また、それをいくつに分けましたか。』
答えを見ると、切り離すたびにバラバラのクラスタとして解釈するらしくて、そうすると辺の数の増え方は、頂点同士を結んで2本、頂点と辺を結んで3本、辺同士を結んで4本増える。
そこから、3回しか分割しない場合は12にしかならず足りないし、7回も分割すると14になり超えてしまう。よって分割回数は4回から6回。
4回の場合は、2本3本4本4本、3本3本3本4本。
5回の場合は、2本2本2本3本4本、2本2本3本3本3本。
6回の場合は、2本2本2本2本2本3本。
頂点同士を結んだ時には内角は増えない。頂点と辺を結んだときには180°増える。辺同士を結んだ時には360°増える。
4回の場合は、どちらにせよ180°×5増えてしまう。6回の場合は180°×1しか増えない。どちらにせよ元々の1.3倍にはならない。
5回の場合は、180°×3増える。それで1.3倍になったわけだから、元々の内角は180°×10。よって12角形だったと分かるらしい。
ステップごとの増加分にだけ着目して、制約で解くということだけど、どう考えれば良いのかな。
いや、もっと原始的な記述でも解けるけど、計算量を減らそうと工夫するとこうなるという話か?「いくつかの多角形」の部分も、マックスを決めればできないことも無いんだが。
こういう問題から、最終的には代数学や解析学なんだろうなあと思うんだよね。代数学とかの群論とか基礎の部分は、コンピューターのメタファーや手元での演算でもう少し簡単になるはずだと思うが。
12年度トライアル問題 問題10
『長方形ABCDの辺BC上にAD=AEとなるようにEを取ります。
いま、AD=12cm、ED=4cmです。このとき、BEの長さを求めなさい。
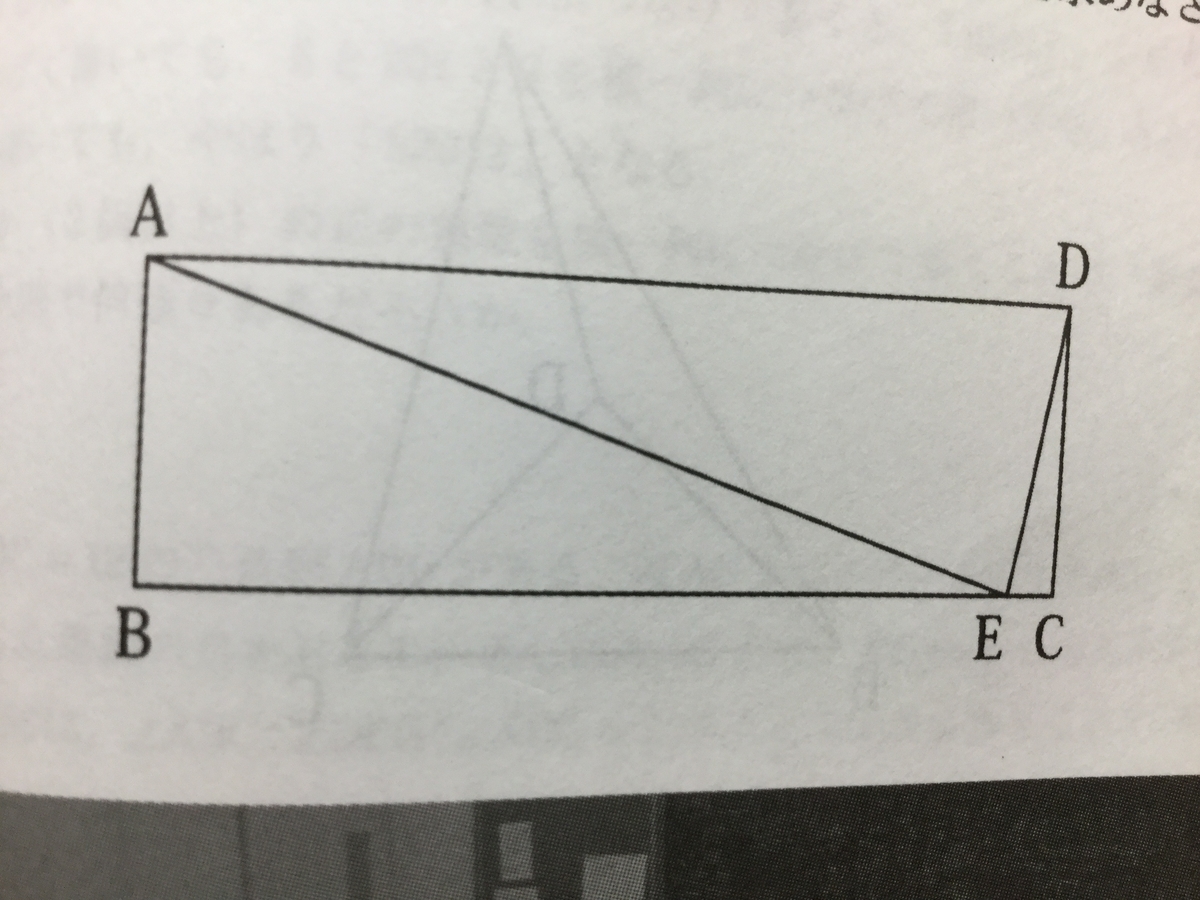 』
』
これは一見既存の種類の問題だが、三角形ADEの角Aから垂線を下ろすという、新しい作図が必要になる。
これが二等辺三角形に限定して良いのか、それとも全ての三角形でこの作図が必要になるのか、今は分からないが、とりあえず前者だと解釈する。
まあ作図の種類を増やせば良いだけなのだが。角度が違うだけなので、方法論としても難しくは無い。
13年度トライアル問題 問題10
『図の四角形ABCDで、点E、F、G、H、MはAE : EB = AF : FD = 2 : 5、BG : GH : HC = 3 : 2 : 2、CM = DMを満たす辺上の点です。いま、EG、FH上にそれぞれEP = PG、FQ = QHとなる点P、Qをとるとき、PQ : BMを求めなさい。
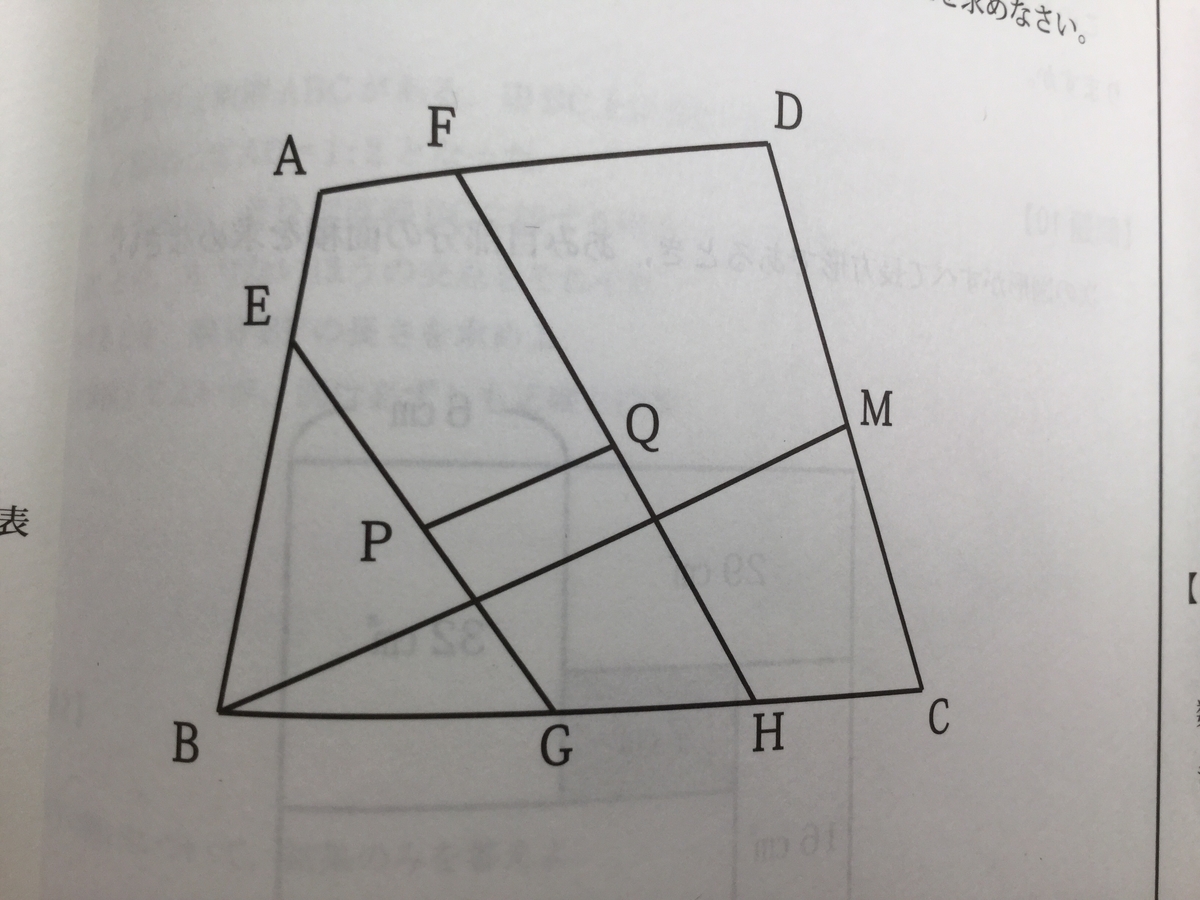 』
』
相似の概念が必要になる。
辺CDに、2:5の点を打って、点F、E、Hとその点を結ぶことで、平行四辺形ができるらしい。
最初は答えを読んでもなぜそうなるのかが分からなかったのだが、対角線を基準に相似で5\7になったり、2\7になったりで、辺の長さが向かい合わせでイコールになるので平行四辺形になるということらしい。
ということで、これからは、二等辺三角形の頂点から垂線を落とす作図に加えて、相似の概念も導入する。
角度が全て同じだったり、全ての辺の比率が同じだったり、同じ角度の角を比率が同じ辺が挟んでいたりしたら、その二つの三角形は相似ということになる。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その30
グラフで表現したユークリッド幾何学の自動解答に挑戦している。ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26 - ニート歴10年からの数学日記までを参考にしている。
12年度ファイナル問題 問題7
『図で、AD=AC、BD=DCです。いま、AD上にPD+FD=BFとなるような点Pをとります。角FAE=24度、角BFD=35度であるとき、角PCDの大きさを求め、考え方も書きなさい。
※ただし、図は正確とは限りません。
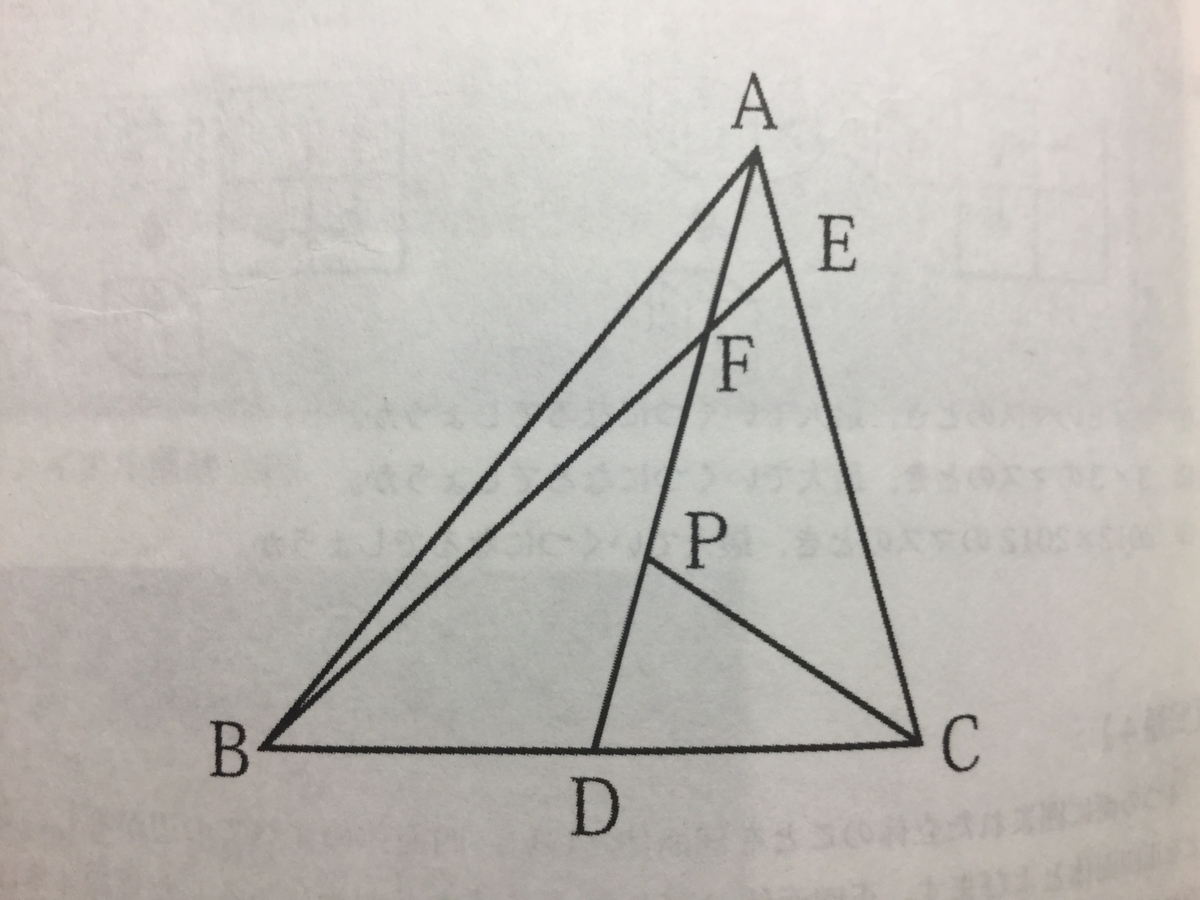 』
』
今回で普通の問題は一段落つけるつもりでいる。今の予定ではだが。
今はプログラムでいう仕様を決めている段階なわけで、一通りの種類の問題をチェックし終わった時に、自動化できるか模索しようと思う。
全体の流れとしては、まず初期条件を設定して、分析して、それからは以下の流れに従う。
「作図」
データ構造を上から見ていって
graphを更新する
平行線リストを更新する
clockwise_lstを更新する
平面上リストを更新する
「分析」
直線の分割による辺の和、角の和
平行線リストによって角のイコール
clockwise_lstによる角の和
三角形の発見
発見した三角形をそのままクラスタに
クラスタが割れているか
三角形定理ループ
「交点の発見」
Aから全ての辺で調べていく (一つの点における平均的な辺の数 ^3 * 点の数)
graphは簡単に更新できる
平行線リストを更新する
clockwise_lstに交点を追加する(交点の場合は他はいじる必要はない)
平面上リストにも交点を追加する
(交点が発生する辺を持つクラスタをどうするかは迷うな、次の分析のステップでやるかどうかが)
(以下、分析、交点の発見、分析、交点の発見、という風に続いていく)
具体的な作図の種類はこんな感じだ。
- ?正四角形の判定
- ?正五角形の判定
では初期条件。
graph := [
A : [
[[B], [], []],
[[F, P, D], [], []],
[[E, C], [], []]
]
,
B : [
[[A], [], []],
[[F, E], [], []],
[[D, C], [], []]
]
,
C : [
[[A, E], [], []],
[[P], [], []],
[[B, D], [], []]
]
,
D : [
[[B], [], [C]],
[[A, F, P], [], []]
]
,
E : [
[[A], [], [C]],
[[B, F], [], []]
]
,
F : [
[[A], [], [P, D]],
[[B], [], [E]]
]
,
P : [
[[A, F], [], [D]],
[[C], [], []]
]
];
parallel_lines_lst := [
];
clockwise_lst := [ #[その辺の記号のgraphの一番最初, 反時計回り側180°, どちらか不明, 時計回り側]
A : [
[E, [], [], [F, B]],
[F, [E], [], [B]],
[B, [E, F], [], []]
]
,
B : [
[A, [], [], [F, D]],
[F, [A], [], [D]],
[D, [A, F], [], []]
]
,
C : [
[B, [], [], [P, A]],
[P, [B], [], [A]],
[A, [B, P], [], []]
]
,
D : [
[B, [C], [], [A, C]],
[A, [B], [], [C]],
[C, [B, A], [], [B]]
]
,
E : [
[C, [A], [], [B, A]],
[B, [C], [], [A]],
[A, [C, B], [], [C]]
]
,
F : [
[B, [E, P], [], [E, A]],
[A, [P, B], [], [P, E]],
[E, [B, A], [], [B, P]],
[P, [A, E], [], [A, B]]
]
,
P : [
[A, [D], [], [D, C]],
[C, [A], [], [D]],
[D, [A, C], [], [A]]
]
];
coplanar_lst := [
[A, B, C, D, E, F, P]
];
triangle_lst := [
];
cluster_lst := [
];
always {
AD == AC;
BD == CD;
DP + DF == BF;
EAF == 24;
PFB == 35;
}
分析に移る。
#単純な辺の和をgraphから生成
#単純な角の和をclockwise_lstから生成
180 == #graphから生成
180 < #clockwise_lstから生成
180 > #clockwise_lstから生成できる
もうこういうのは飛ばしちゃおう、これだけ書いて。
平行線リストは無し。
三角形の発見、
発見した三角形をそのままクラスタに、
クラスタが割れているか、
も飛ばしちゃおう。
で三角形定理ループ。
分析自体は、もうやろうと思えば自動化できる。交点の発見も、発見するだけならおそらく自動化できると思う。論点は一つ一つの作図だろう。
では作図に移る。作図は、
graphを更新する
平行線リストを更新する
clockwise_lstを更新する
平面上リストを更新する
というステップを踏むんだった。
じゃあ、BとPを結んでみよう。
graphの更新は当たり前にできるだろう。平行線リストも平面上リストも特に変更は無い。
問題はclockwise_lstの更新だ。考えるために、元々のclockwise_lstから引用する。
B : [
[A, [], [], [F, D]],
[F, [A], [], [D]],
[D, [A, F], [], []]
]
P : [
[A, [D], [], [D, C]],
[C, [A], [], [D]],
[D, [A, C], [], [A]]
]本当はE以外の全ての点を共有しているのだが。
これは、例えばAとCで同じ時計回り同士だと、AとCのどちらが内側かが分からない。位置を入れ替えることができるんで、どの角の間にあるのかの参考にならない。
まあ180°以下かどうか確かめる必要はあるが、FBDがポジティブな所から、しっかりFとD(P側だとDとA)の間だと分かるだろう。
で分析して、更には交点を探したり何だりする。
次は辺の延長。交点は後から探すしどこでも良いのだけど、ADと同じだけAから延ばしてみようか。
graphを更新して、平面上リストに新しい点を追加して、平行線リストは特に何も無くて。
これも問題は、clockwise_lstだろう。考えるために引用する。
A : [
[E, [], [], [F, B]],
[F, [E], [], [B]],
[B, [E, F], [], []]
]新しい点をGとすると、Fの左と右をひっくり返したような、「[G, [B, F], [], [E, F]]」という風になるのだと思う。
で性質上、EやBにおいてはFの反対側に来る。つまりこうなる。
A : [
[E, [G], [], [F, B]],
[F, [E, G], [], [B, G]],
[B, [E, F], [], [G]],
[G, [B, F], [], [E, F]]
]これで分析して、交点を探せば良いだろう。
次は二等辺三角形の作図。2つの角を比較して、大きい側と小さい側で2種類の作図がある。
三角形AEFをモデルにしよう。角Aは24°だし、角Fは角BFDの対頂角なので、35°だ。
△AEF : [EAF, AE, FEA, EF, EFA, AF]
EAF == 24
EFA == 35
じゃあ2つの角を比較して、EAF < EFAが明らかになったとする。
まず小さい方の角の作図から検討する。小さい方の角と頂点の間に、底辺のもう一方の端点から辺を引いて、二等辺三角形を作図する。
つまり、辺AEの間に、点Fから辺を引く。新しい点はGとする。
graph := [
A : [
[[B], [], []],
[[F, P, D], [], []],
[[E, C, G], [], []]
]
,
E : [
[[A, G], [], [C]],
[[B, F], [], []]
]
,
F : [
[[A], [], [P, D]],
[[B], [], [E]],
[[G], [], []]
]
,
G : [
[[A], [], [E, C]],
[[F], [], []]
]まあ、このCは、つまりgraphにおける辺の上の点の順番は、調べれば分かるだろう。
平行線リストも平面上リストも、そんなに複雑では無い。
問題は、やはりclockwise_lstだろう。
三角形としては時計回りで、A, E, F, A, E, Fというような順番になっているわけだが。
clockwise_lst := [ #[その辺の記号のgraphの一番最初, 反時計回り側180°, どちらか不明, 時計回り側]
F : [
[G, [A], [B, P], [E]],
[B, [E, P], [G], [E, A]],
[A, [P, B], [], [P, E, G]],
[E, [B, A, G], [], [B, P]],
[P, [A, E], [G], [A, B]]
]
,
G : [
[E, [A], [], [F, A]],
[F, [E], [], [A]],
[A, [E, F], [], [E]]
]Gにおいては、AとEの時計回りで先側から、E, F, Aの順番になる。
Fにおいては、Aからは時計回り側、Eからは反時計回り側にGがあるのは確定。
で本当は、BやPにおいても、ちょっと見にくいがそれぞれEやAをひっくり返しただけなので、確定するはずなのだが。
ちょっと脱線するが、clockwise_lstにおける、不確定な点の位置の絞り込みについて考えてみたい。
結果的に、最初はどれでも良いが例えばB, A, G, E, Pの順番なので、下のような順番になってほしい。とりあえず並び替えただけだが。
clockwise_lst := [ #[その辺の記号のgraphの一番最初, 反時計回り側180°, どちらか不明, 時計回り側]
F : [
[B, [E, P], [G], [E, A]],
[A, [P, B], [], [P, E, G]],
[G, [A], [B, P], [E]],
[E, [B, A, G], [], [B, P]],
[P, [A, E], [G], [A, B]]
]思考回路としては、一番制約が強いEとAの、とりあえずAに着目して、それからEとの整合性を取る感じなのかな?
F : [
[B, [E, P], [G], [E, A]],
[A, [P, B], [], [P, E, G]],
[G, [A], [B, P], [E]]
[E, [B, A, G], [], [B, P]],
[P, [A, E], [G], [A, B]],
]循環リストで、Aから後ろ2つにPとBがあって、Aから前3つにPとEとGがある、というような制約なのだけど。
位置の制約と呼んでいたっけか。記述法はもう忘れたけど。
とにかく、そういう制約と、後は例えばBFGが180°以上か以下か。180°以上だったらBにおいてはGを右に振り分けて、以下だったら左に振り分ける。
角度が明らかになって、その方法で制約がハッキリすることもあるだろうから、この絞り込みのセクションは作図とは別に設けたほうが良いだろう。
もう一方の二等辺三角形の作図も、似たようなものになるだろう。次の作図に行く。
クラスタの貼り合わせをする。じゃあその、三角形AEFをクラスタと捉えることにしよう。
[[A, E, F], [EAF, AE, FEA, EF, EFA, AF]]
例えばAEで、三角形AEFとそのコピー、三角形AEGを貼り合わせるとする。
同じ長さの辺で、4種類の貼り付け方がある。今回はコピーなので、3種類だろうが。
同じ方向の2種類は、角度や辺の大きさの対応で分ければ良いのかな。同じ側は[A, E, G]で、反対側は[E, A, G]になるだろう。
クラスタからグラフを生成することは簡単だろうし、平行線リストも平面上リストも、まあそこまでは難しくないだろう。やはり問題はclockwise_lstだ。
まあ反対側に作る場合は、こんな感じじゃないだろうか。
clockwise_lst := [
A : [
[G, [], [B, F], [E]],
[E, [G], [], [F, B]],
[F, [E], [G], [B]],
[B, [E, F], [G], []]
]
,
E : [
[G, [A], [C, B], []],
[C, [A], [G], [B, A]],
[B, [C], [G], [A]],
[A, [C, B], [], [C, G]]
]
];AにおけるEでは、Fの反対側にあるのは確定。他はBはもちろん、Fですら180°のどちらかは分からないんじゃないか。後から角度とかで絞り込めば良い。
Eにおいても、似たような感じだろう。
次は同じ側に作る場合。
clockwise_lst := [
A : [
[G, [E], [F, B], []],
[E, [], [], [F, B, G]],
[F, [E], [G], [B]],
[B, [E, F], [G], []]
]
,
E : [
[G, [], [C, B], [A]],
[C, [A], [G], [B, A]],
[B, [C], [G], [A]],
[A, [C, B, G], [], [C]]
]
];今度は逆に、AにおけるEとかで同じ側にあるのが確定って感じじゃないか。他はBとかはもちろん、Fも分からないんじゃないか、どちらの角が大きいかっていうのは。
こんな感じで良いだろう。次回は算数オリンピックの同じような問題から変な問題を見つけるか、ジュニア算数オリンピックの面積の問題をやるか、じゃないか。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その29
グラフで表現したユークリッド幾何学の自動解答に挑戦している。ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26 - ニート歴10年からの数学日記までを参考にしている。
09年度トライアル問題 問題10
『図で、AB = AE、DC = DEで、ABとDEは平行です。
また、角DAE = 53°、角AED = 106°、角CDE = 42°になっています。
このとき、角EBCの大きさを求めなさい。
(※図は正確ではありません。)
 』
』
昨日の続きというか、角度のポジティブやネガティブを廃止して、時計回り順番で例えば角ABCと角CBAのように区別できないか、を挑戦するんだった。
しかし考えてみれば、anglewise_lst(時計回りリスト)における先とは何だろうか。先の方に存在すると言っても、一周回ってしまうのだから、後の方に存在するでもあるんじゃないか。
まあそう考えてみると、やはり180°という基準は必要ではあるのかもしれない、辺を基準に反対側の直線までという意味で。180°以上の角が存在する場合も、そういう角が2つできることは無いのだから、単に循環リストの前と後ろをくっつけるだけで良いだろう(いや厳密には循環リストですら無いのか、当初はともかく、今やその辺より前か後かで相対的に順番を記述しているのだから)。
人間がやるように、問題文を入力する際にポジティブやネガティブかを判別して入力できるというのも大きい。ただ、その記述を採用するならば、ますますangle_lstはいらないのではないか、という気もする。まあとにかく試してみなければ分からないだろう。
では初期条件。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
}
元々あったangle_lstのEと見比べてみよう。
angle_lst := [
E : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
]
];
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
まあ細かい手順はともかく、工夫すれば置き換え可能そうな雰囲気が伝わってくる。この設定で進めてみよう。
休憩から明けてみて、やっぱり循環リストっていうのは並び方を変えても成立するものじゃないといけないわけで、clockwise_lstを前に戻すことは考えられないという気分だ。
始めてみて分かったけど、今日はイージーモードだな、ほとんど昨日のをコピペすれば良いわけだから。
では続き。
graphから辺の和や180°の角の和は無し。
parallel_lines_lst(とgraph)から、EAB == AED; #同じ大きさの対頂角・錯角の4角ずつが2セットあり得るわけだが、一方は貫く辺が先に来て、もう一方は貫かれる辺が先に来る。「キ」の字のような手元の図をどれだけ回しても、その関係は変わらない。まあよく考えてないが、多分大丈夫だろう
clockwise_lstから、
DAE + EAB == DAB、EAB + BAD == EAD、BAD + DAE == BAE、
みたいなのを延々と作っていく。まあ話が分かりやすくはなった。全部は書かない。
graphから、△ADE
△ABE
△BCE
△CDE
更にそれで登録した三角形から、ほぼそのままcluster_lstに登録
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]] #今回は点の並べ方が時計回りだけど、点の並べ方は反時計回りの方が、角とか辺が単純な見た目になる
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]] #例えばこのA, B, Eの順番は反時計回り。よく考えたらgraphを確認しなきゃいけないから、だからどうしたという話かもしれん
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]] #まあでもその場合も、graphでの一番最初に登録した同じ方向の点に置き換えれば良いだけだから、やっぱり簡単は簡単
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]] #作業は単純であるに越したことは無い。しかしプログラムだと考えない方が単純なんだよなあ
それらが全部終わってから、三角形定理ループを回す。しかし、どう明らかになるかはこの環境では分からない。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
}
作図
このままでは解答に至らないらしいので、作図に移る。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その25 - ニート歴10年からの数学日記、
セットアップ時の角の和の取得法について - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その21 - ニート歴10年からの数学日記の後半、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その18 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その17 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その16 - ニート歴10年からの数学日記、
辺りを参考にする、後ろに行くほどもう参考にならないと思うけど。
- ?正四角形の判定
- ?正五角形の判定
作業の流れはこんな感じだ。
「作図」
データ構造を上から見ていって
graphを更新する
平行線リストを更新する
clockwise_lstを更新する
平面上リストを更新する
「分析」
辺の和、直線の分割による角の和
平行線リストによって角のイコール
clockwise_lstによる角の和
三角形の発見
発見した三角形をそのままクラスタに
クラスタが割れているか
三角形定理ループ
「交点の発見」
Aから全ての辺で調べていく (一つの点における平均的な辺の数 ^3 * 点の数)
graphは簡単に更新できる
平行線リストを更新する
clockwise_lstに交点を追加する(交点の場合は他はいじる必要はない)
平面上リストにも交点を追加する
(交点が発生する辺を持つクラスタをどうするかは迷うな、次の分析のステップでやるかどうかが)
(以下、分析、交点の発見、分析、交点の発見、という風に続いていく)
では、点と点を結ぶ。今回もAとCを結ぶことにする。以下もほとんどコピペ。
graphのAとCにそれぞれ追加する。
次に、clockwise_lstの例えばAにおいて、CはDやEやBとどのような位置関係にあるか。
幸いそれぞれにおいて、AとCはそれぞれ繋がっている。だから位置関係も分かる。
(これは手元に図を描いて書いているのだが、いや今回は描いて無いのだが、)例えばDだと、時計回りでCからAからの順番なので、AにおいてCは、Dから時計回りで進んだ側にある。
Eだと、時計回りでAからCの順番なので、AにおいてCは、Eから時計回りで戻った側にある。
Bだと、時計回りでAからCの順番なので、AにおいてCは、Bから時計回りで戻った側にある。
つまり、
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]という風になるはずだ。
Cにおいてはそれぞれ逆なので、
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]という風になるはずだ。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
}
次に分析。またコピペする。
新しい辺の和や180°の角の和は無し。
clockwise_lstから新しい角を登録する。
次にgraphから三角形を探す。
結果、△ABC、△ACD、△ACEが見つかるはずだ。
そのままクラスタに登録する。
更に、クラスタの分割をチェックするが、分割されても三角形になるだけなので無視する。
三角形定理ループを回す。この環境では分からない。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE],
△ABC : [CAB, AB, ABC, BC, BCA, AC],
△ACD : [DAC, AC, ACD, CD, CDA, AD],
△ACE : [CAE, AC, ECA, CE, AEC, AE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, B, C], [CAB, AB, ABC, BC, BCA, AC]],
[[A, C, D], [DAC, AC, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AC, ECA, CE, AEC, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
}
三角関数で交点のチェックをする。計算量的に可能なうちは、全ての辺の組み合わせでチェックする。それが無理になってきたら、作図したり新しく明らかになったたびに、それだけチェックする。でもそうすると、グローバル変数だとかでデータ構造を扱う必要が出てくるのではないか、という気もする。キュー(リストを待ち行列のように使う)でタスクを管理すれば、そうでもないか。
以下ほぼコピペ。
そうすると、ACとDEの間に交点ができるのが分かるはず。それをFと名付ける。
交点なので、graphは簡単に更新できる。
平行線リストも更新する。
clockwise_lstにFを作る。
交点なので、他の点では手を加える必要は無い。また全ての角はポジティブなはずなので、どれを最初に持ってくるかは適当で良いだろう。
時計回りで「A, D, C, E」なのか「A, E, C, D」なのかは、交点を発見するのに使った三角を基準に考えれば良いだろう、多分。
180°ピッタリはどう登録しよう。両方に登録しようか。
平面上リストにも点Fを追加する。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C, F], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E, F], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D, F], [], []]
]
,
F : [
[[A], [], [C]],
[[D], [], [E]]
]
];
parallel_lines_lst := [
[[A, B], [D, F, E]] #今回はDEの間で良かったけど、これも順番が分からないこともあるのかもな
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
,
F : [
[A, [E, C], [], [D, C]],
[D, [A, E], [], [C, E]],
[C, [D, A], [], [E, A]],
[E, [C, D], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE],
△ABC : [CAB, AB, ABC, BC, BCA, AC],
△ACD : [DAC, AC, ACD, CD, CDA, AD],
△ACE : [CAE, AC, ECA, CE, AEC, AE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, B, C], [CAB, AB, ABC, BC, BCA, AC]],
[[A, C, D], [DAC, AC, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AC, ECA, CE, AEC, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
}
分析。またコピペ。
辺の和
AF + CF == AC; DF + EF == DE;
180°の角の和
AFC
CFA
DFE
EFD
()
clockwise_lstから角の和
三角形
△AFD
△AFE
△CFD
△CFE
そのままクラスタに
[[A, F, D], [DAC, AF, AFD, DF, EDA, AD]]
[[A, F, E], [CAE, AF, EFA, EF, AED, AE]]
[[C, F, D], [ACD, CF, DFC, DF, CDE, CD]]
[[C, F, E], [ECA, CF, CFE, EF, DEC, CE]]
クラスタ割れているか 辺ACと辺DEにFを加えて
AF, AFC, CF
DF, DFE, EF
なので
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, B, C], [CAB, AB, ABC, BC, BCA, AC]],
[[A, C, D], [DAC, AC, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AC, ECA, CE, AEC, AE]]
から
[[A, B, E, F, D], [DAB, AB, ABE, BE, BED, EF, EFD, DF, EDA, AD]],
[[A, D, F, E], [DAE, AD, EDA, DF, DFE, EF, AED, AE]],
[[C, D, F, E], [ECD, CD, CDE, DF, DFE, EF, DEC, CE]],
[[A, B, C, F], [CAB, AB, ABC, BC, BCA, CF, CFA, AF]],
[[A, C, D], [DAC, AF, AFC, CF, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AF, AFC, CF, ECA, CE, AEC, AE]]
三角形定理ループを回す。けどこの環境では無理。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C, F], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E, F], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D, F], [], []]
]
,
F : [
[[A], [], [C]],
[[D], [], [E]]
]
];
parallel_lines_lst := [
[[A, B], [D, F, E]] #今回はDEの間で良かったけど、これも順番が分からないこともあるのかもな
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B], [], [D, C]],
[D, [B, A], [], [C]],
[C, [A, D], [], [B]],
[B, [C], [], [A, D]]
]
,
F : [
[A, [E, C], [], [D, C]],
[D, [A, E], [], [C, E]],
[C, [D, A], [], [E, A]],
[E, [C, D], [], [A, D]]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE],
△ABC : [CAB, AB, ABC, BC, BCA, AC],
△ACD : [DAC, AC, ACD, CD, CDA, AD],
△ACE : [CAE, AC, ECA, CE, AEC, AE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[A, F, D], [DAC, AF, AFD, DF, EDA, AD]],
[[A, F, E], [CAE, AF, EFA, EF, AED, AE]],
[[C, F, D], [ACD, CF, DFC, DF, CDE, CD]],
[[C, F, E], [ECA, CF, CFE, EF, DEC, CE]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, B, C], [CAB, AB, ABC, BC, BCA, AC]],
[[A, C, D], [DAC, AC, ACD, CD, CDA, AD]],
[[A, C, E], [CAE, AC, ECA, CE, AEC, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
AF + CF == AC;
DF + EF == DE;
}
新しい作図に入る。次は線の同じ長さ分だけの延長をやる。データの状態をリセットする。
昨日と同じように、辺CEをEの方向に延長する。先端にできる新しい点はFと名付ける。以下ほとんどコピペ。
まずgraphを更新する。CとEを更新して、また点Fを作る。
平行線リストの更新は無し。
次にclockwise_lstを更新する。Eを更新して、また点Fを作る。
Eにおいては、Cから180°なので、Cの両方にFを入れる。EにおけるF自体も、ちょうどそのように配置する。Eにおける他もそれに合わせる。
今回はおそらく偶然に上手く行った。
平面上リストにもFを追加する。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F]],
[[D], [], []]
]
,
F : [
[[C, E], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B, F], [], [D, C]],
[D, [B, A, F], [], [C]],
[C, [A, D, F], [], [B, F]],
[B, [C], [], [A, D, F],
[F, [B, C], [], [A, D, C]]]
]
,
F : [
[C, [], [], []]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
CE == EF;
}
作図はしたので分析に入る。コピペ。
辺の和
CE + EF == CF;
180°の角
CEF、FEC
平行線リストによる角のイコールは、交点がまだ発生してないので無し
三角形は、探してないが、Eから伸ばしただけなのでどうせ無い。
だから新しくクラスタとして登録する三角形は無し
またクラスタの分割も、クラスタ内で新しく点と点が繋がるということは無いはずなので、無し
三角形定理ループを回す。しかしこの環境では結果は分からない
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F]],
[[D], [], []]
]
,
F : [
[[C, E], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B, F], [], [D, C]],
[D, [B, A, F], [], [C]],
[C, [A, D, F], [], [B, F]],
[B, [C], [], [A, D, F],
[F, [B, C], [], [A, D, C]]]
]
,
F : [
[C, [], [], []]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
CE == EF;
CE + EF == CF;
}
交点の発見に入る。全部の辺の組み合わせを調べる。辺ABとの間にできることが分かるだろう。
ABとEFの交点Gを作図する。
まずgraphを更新する。
平行線リストも更新する。
clockwise_lstも更新する。実はG以外はイジる必要が無い。graphにおいて他は後から付け加えているだけなので。
発見時の三角を参考にすれば、登録できると思う、多分ね。
平面上リストも更新する。
で、前回と同じくクラスタも更新する。辺ABを含むものについて。
A, B → A, G, B
AB → AG, AGB, BG
あるいは
B, A → B, G, A
AB → BG, BGA, AG
(しかし後者は必要無かった)
もともとが
[[A, B, C, D], [DAB, AB, ABC, BC, BCD, CD, CDA, AD]],
[[A, B, E, D], [DAB, AB, ABE, BE, BED, DE, EDA, AD]],
[[A, B, E], [EAB, AB, ABE, BE, BEA, AE]],
でこうなる
[[A, G, B, C, D], [DAB, AG, AGB, BG, ABC, BC, BCD, CD, CDA, AD]],
[[A, G, B, E, D], [DAB, AG, AGB, BG, ABE, BE, BED, DE, EDA, AD]],
[[A, G, B, E], [EAB, AG, AGB, BG, ABE, BE, BEA, AE]],
graph := [
A : [
[[B, G], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F, G], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F, G]],
[[D], [], []]
]
,
F : [
[[C, E, G], [], []]
]
,
G : [
[[A], [], [B]],
[[F], [], [E, C]]
]
];
parallel_lines_lst := [
[[A, G, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B, F], [], [D, C]],
[D, [B, A, F], [], [C]],
[C, [A, D, F], [], [B, F]],
[B, [C], [], [A, D, F],
[F, [B, C], [], [A, D, C]]]
]
,
F : [
[C, [], [], []]
]
,
G : [
[F, [B, E], [], [A, E]],
[A, [F, B], [], [E, B]],
[E, [A, F], [], [B, F]],
[B, [E, A], [], [F, A]]
]
];
coplanar_lst := [
[A, B, C, D, E, F, G]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE]
];
cluster_lst := [
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, G, B, C, D], [DAB, AG, AGB, BG, ABC, BC, BCD, CD, CDA, AD]],
[[A, G, B, E, D], [DAB, AG, AGB, BG, ABE, BE, BED, DE, EDA, AD]],
[[A, G, B, E], [EAB, AG, AGB, BG, ABE, BE, BEA, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
CE == EF;
CE + EF == CF;
}
分析する。以下もコピペ。
辺の和
CE + EG == CG;
AG + BG == AB;
FG + EG == EF;
FG + CG == CF;
180°の角
CEG
GEC
AGB
BGA
EGF
FGE
平行線リストによって角のイコール。ぶっちゃけ手順は忘れた
GED == EGB;
GED == FGA;
DEC == AGE;
DEC == BGF;
clockwise_lstによる角の和。面倒なので勝手に登録してくれてると見なす。手順は単純だろうし。
三角形の発見
△AEG
△BCG
△BEG
発見した三角形をそのままクラスタに
[[A, E, G], [EAB, AE, FEA, EG, AGE, AG]]
[[B, C, G], [ABC, BC, BCE, CG, EGB, BG]]
[[B, E, G], [ABE, BE, BEF, EG, EGB, BG]]
クラスタが割れているか 今回はGだけを確認すれば良いみたいだ
[A, G, B, C, D]
CG
[A, G, C, D]
[G, B, C]
[[A, G, C, D], [DAB, AG, AGE, CG, ECD, CD, CDA, AD]]
[A, G, B, E, D]
EG
[A, G, E, D]
[G, B, E]
[[A, G, E, D], [DAB, AG, AGE, EG, FED, DE, EDA, AD]]
三角形定理ループを回す。この環境だと無理だが
graph := [
A : [
[[B, G], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F, G], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F, G]],
[[D], [], []]
]
,
F : [
[[C, E, G], [], []]
]
,
G : [
[[A], [], [B]],
[[F], [], [E, C]]
]
];
parallel_lines_lst := [
[[A, G, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [B, F], [], [D, C]],
[D, [B, A, F], [], [C]],
[C, [A, D, F], [], [B, F]],
[B, [C], [], [A, D, F],
[F, [B, C], [], [A, D, C]]]
]
,
F : [
[C, [], [], []]
]
,
G : [
[F, [B, E], [], [A, E]],
[A, [F, B], [], [E, B]],
[E, [A, F], [], [B, F]],
[B, [E, A], [], [F, A]]
]
];
coplanar_lst := [
[A, B, C, D, E, F, G]
];
triangle_lst := [
△ADE : [DAE, AD, EDA, DE, AED, AE],
△ABE : [EAB, AB, ABE, BE, BEA, AE],
△BCE : [EBC, BC, BCE, CE, CEB, BE],
△CDE : [ECD, CD, CDE, DE, DEC, CE],
△AEG : [EAB, AE, FEA, EG, AGE, AG],
△BCG : [ABC, BC, BCE, CG, EGB, BG],
△BEG : [ABE, BE, BEF, EG, EGB, BG]
];
cluster_lst := [
[[A, E, C, D], [DAE, AE, AEC, CE, ECD, CD, CDA, AD]],
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
[[B, C, E], [EBC, BC, BCE, CE, CEB, BE]],
[[C, D, E], [ECD, CD, CDE, DE, DEC, CE]],
[[A, G, B, C, D], [DAB, AG, AGB, BG, ABC, BC, BCD, CD, CDA, AD]],
[[A, G, B, E, D], [DAB, AG, AGB, BG, ABE, BE, BED, DE, EDA, AD]],
[[A, G, B, E], [EAB, AG, AGB, BG, ABE, BE, BEA, AE]],
[[A, E, G], [EAB, AE, FEA, EG, AGE, AG]],
[[B, C, G], [ABC, BC, BCE, CG, EGB, BG]],
[[B, E, G], [ABE, BE, BEF, EG, EGB, BG]],
[[A, G, C, D], [DAB, AG, AGE, CG, ECD, CD, CDA, AD]],
[[A, G, E, D], [DAB, AG, AGE, EG, FED, DE, EDA, AD]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
EAB == AED;
#単純な角の和をclockwise_lstから生成しなければいけないんだが、面倒なので書きたくない。支障は無いだろう
180 == #graphから生成する
180 > #clockwise_lstから生成する
180 < #生成できるけど生成しなくても良いかもしれない
CE == EF;
CE + EF == CF;
CE + EG == CG;
AG + BG == AB;
FG + EG == EF;
FG + CG == CF;
GED == EGB;
GED == FGA;
DEC == AGE;
DEC == BGF;
}
次の作図に行く。前回においては二等辺三角形の作図を飛ばして、クラスタの作図に行っているので、今回もそうする。コピペする。
△ADEのクラスタを、DEで回転させるように貼り付ける。新しい点をFとする。
[[A, D, E], [DAE, AD, EDA, DE, AED, AE]],
から
[[F, D, E], [EFD, DF, FDE, DE, DEF, EF]],
みたいなのを複製したい。
つまり今回は、角における位置がそれぞれ入れ替わるわけだ。
他は良いんだけど、angle_lstが難しい。
新しく作るFはAにおけるDとEの順番を反転させるだけで良い。しかしDとEは、例えばDの角において、Eを基準にAが時計回りで先側にあるなら、反転させたら戻った側にあるとは言えるが、それ以上言えるだろうか。
人間は、見た目や実際の角度を参考にして判断するわけだが。
反対側に辺を延長する作図ほどは単純じゃなくて、やっぱり大きさの比較が必要になる。
今まではclockwise_lstの点に属する辺の一つ一つは、「[[時計回り反時計回りのどちらか], [隣り合う可能性がある], [時計回り反時計回りのどちらか]]」というつもりだった。
しかし、「[[時計回り反時計回りのどちらか], [両方のどちらか分からない], [時計回り反時計回りのどちらか]]」にすべきかと考えている。
あるいは、「[[時計回り反時計回りのどちらか], [隣り合う可能性がある], [時計回り反時計回りのどちらか], [両方のどちらか分からない]]」でも良いかもしれない。
大は小を兼ねるというか、そうすると、人間が初期条件でポジティブかネガティブか判断できないという想定でも、全てをどちらか分からないに入れず、現に隣り合っているものを隣り合う可能性があるに入れることで、やりやすくなるはず。両方に隣り合う可能性があるものがあれば、そこにあるのだろうという感じで。新しく辺を付ける時は可能性が追加される感じで、消せる可能性はどんどん消していく。
右隣に隣り合う可能性があるとか、左隣に隣り合う可能性があるとか、そういう風に細かく分けても良いけど、どうしようかな。
「[[反時計回りに180°以内], [隣り合う可能性がある], [時計回りに180°以内], [両方のどちらか分からない]]」というのが現在の第一候補ではある。
「[[反時計回りに180°以内], [反時計回りで隣り合う可能性がある], [時計回りで隣り合う可能性がある], [時計回りに180°以内], [両方のどちらか分からない]]」という風にするかどうかで迷っている。明らかにクドいんだよなあ。反時計回りと時計回りで使い分けることがあるか、ってことなんだけど。
まあ別に、そうした所で2回登録する必要があるだけで、思考に混乱があるわけじゃないから、念の為にそちらを採用してみようか。次回からはそうしよう。
ああいや、時計回り反時計回りのどちらか、からの変更も考えなければいけないのか。いやとにかく迷った二つのうちの後者を試して、様子を見て前者に切り替えて、その時にそこをきっちりするかを考えれば良い。
いや、どうしようかなあ。例えば反時計回りで隣り合っている場合は、「[..., 隣り合う一方], [..., 隣り合う一方], [...], [...], [...]」という感じになるんだろうか。
隣り合う可能性があると、どちらかの方向に180°以内にあるは、違う概念なんじゃないか。どうせ180°以内とか、どちらか分からないとか、記述するのだから、迷った内の後者は意味が無いのではないか。
それならば、「[[反時計回りに180°以内], [隣り合う可能性がある], [時計回りに180°以内], [両方のどちらか分からない]]」かな。
反時計回り、時計回りでハッキリさせるのかも考える必要があるし。
寝不足なせいか分からない。どれが良いかいつかは定まると思うけど。
「[[時計回り反時計回りのどちらか], [両方のどちらか分からない], [時計回り反時計回りのどちらか]]」が基本として、時計回り反時計回りでハッキリさせるか、隣り合う可能性があるという項を入れるか、の二つを考える必要があるということだろうが。
とりあえずその基本で行くと、今回はこうなるだろう。
D : [
[F, [], [C, E, A], []],
[C, [], [F], [E, A]],
[E, [C, F], [], [A]],
[A, [C, E], [F], []]
]
,
E : [
[F, [], [A, D, C, B], []],
[A, [B], [F], [D, C]],
[D, [B, A], [], [C, F]],
[C, [A, D], [F], [B]],
[B, [C], [F], [A, D]]
]
まずDにおいて、Eから見たAの反対側にFがあるはずだ。Eにおいても、Dから見たAの反対側にFがあるはずだ。
Dにおいて、Aから見たEの反対側にFがあるとは、当たり前だが言えないだろう。間違えたけど、実際に同じ方向にある。
(Fから見たEは?)
まあEを中心としたAとFの角は、角度が212と168なんで、そこら辺から判断が付くんじゃないかと思うが。AEFとかFEAで180°以上か以下かを調べれば良い。
風邪気味らしくて、寝て起きて今書いているけど、いろいろと駄目だな。
見た目的には時計回りで隣り合っていても、角度が分からないなら反時計回り側の180°にあるかもしれないわけで、[隣り合う可能性がある]とその180°だけで、[時計回り側で隣り合う可能性がある]を表現することはできない。
その上で、角度を調べるということなら、あの基本形に加えて、時計回りか反時計回りかをハッキリさせて、その上でFEAが180°以下だったら、Fの右辺の時計回り側にAを挿入して、Aの左辺の反時計回り側にFを挿入する、という風にすれば良いだろう。AEFは360 - FEAで登録してあるので、調べなくても良い。その作業を、不確定なものごとにやっていけば良い。
EにおいてはDの条件からもう少し絞れるだろう。
まあ、今日はここまでで良いかな。形式も変わることだし。次回どうするかは明日決める。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その28
グラフで表現したユークリッド幾何学の自動解答に挑戦している。ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26 - ニート歴10年からの数学日記までを参考にしている。
09年度トライアル問題 問題10
『図で、AB = AE、DC = DEで、ABとDEは平行です。
また、角DAE = 53°、角AED = 106°、角CDE = 42°になっています。
このとき、角EBCの大きさを求めなさい。
(※図は正確ではありません。)
 』
』
では初期条件。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B]],
[D, [A], [], [C, B]],
[C, [A, D], [], [B]],
[B, [A, D, C], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, B, E, D], [BAD_p, AB, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
}
graphから辺の和や180°の角の和は無し。
parallel_lines_lst(とgraph)から、BAE_p == AED_p;
angle_lstから、DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
graphから、△ADE
△ABE
△BCE
△CDE
更にそれで登録した三角形から、ほぼそのままcluster_lstに登録
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]]
[[A, B, E], [BAE_p, AB, ABE_p, BE, AEB_p, AE]]
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]]
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
それらが全部終わってから、三角形定理ループを回す。しかし、どう明らかになるかはこの環境では分からない。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B]],
[D, [A], [], [C, B]],
[C, [A, D], [], [B]],
[B, [A, D, C], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE]
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, B, E, D], [BAD_p, AB, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[A, B, E], [BAE_p, AB, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
}
作図
このままでは解答に至らないらしいので、作図に移る。
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その26 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その25 - ニート歴10年からの数学日記、
セットアップ時の角の和の取得法について - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その21 - ニート歴10年からの数学日記の後半、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その18 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その17 - ニート歴10年からの数学日記、
ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その16 - ニート歴10年からの数学日記、
辺りを参考にする、後ろに行くほどもう参考にならないと思うけど。
- ?正四角形の判定
- ?正五角形の判定
では、点と点を結ぶ。今回はAとCを結ぶことにする。
graphのAとCにそれぞれ追加する。
次に、angle_lstの例えばAにおいて、CはDやEやBとどのような位置関係にあるか。
幸いそれぞれにおいて、AとCはそれぞれ繋がっている。だから位置関係も分かる。
(これは手元に図を描いて書いているのだが、)例えばDだと、時計回りでCからAからの順番なので、AにおいてCは、Dから時計回りで進んだ側にある。
Eだと、時計回りでAからCの順番なので、AにおいてCは、Eから時計回りで戻った側にある。
Bだと、時計回りでAからCの順番なので、AにおいてCは、Bから時計回りで戻った側にある。
つまり、
A : [
[
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
]という風になるはずだ。
Cにおいてはそれぞれ逆なので、
C : [
[
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
]という風になるはずだ。
clockwise_lstでも同じように登録する。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B]],
[D, [A], [], [C, B]],
[C, [A, D], [], [B]],
[B, [A, D, C], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE]
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, B, E, D], [BAD_p, AB, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[A, B, E], [BAE_p, AB, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
}
新しい辺の和や180°の角の和は無し。
angle_lstから、CAD_p + CAE_p == DAE_p;
CAD_p + BAC_p == BAD_p;
ACB_p + ACD_p == BCD_p;
ACE_p + ACD_p == DCE_p;
次にgraphから三角形を探す。
結果、△ABC、△ACD、△ACEが見つかるはずだ。
そのままクラスタに登録する。
更に、クラスタの分割をチェックするが、分割されても三角形になるだけなので無視する。
三角形定理ループを回す。この環境では分からない。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B]],
[D, [A], [], [C, B]],
[C, [A, D], [], [B]],
[B, [A, D, C], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
]
];
coplanar_lst := [
[A, B, C, D, E]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE],
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△ACD : [CAD_p, AC, ACD_p, CD, ADC_p, AD],
△ACE : [CAE_p, AC, ACE_p, CE, AEC_p, AE]
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, B, E, D], [BAD_p, AB, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[A, B, E], [BAE_p, AB, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[A, C, D], [CAD_p, AC, ACD_p, CD, ADC_p, AD]],
[[A, C, E], [CAE_p, AC, ACE_p, CE, AEC_p, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
CAD_p + CAE_p == DAE_p;
CAD_p + BAC_p == BAD_p;
ACB_p + ACD_p == BCD_p;
ACE_p + ACD_p == DCE_p;
}
で、三角関数での交点のチェック。
angle_lstのACで調べるのはもちろん、Aにおける他のD、E、Bにおいても、調べていく。Cにおける他でも調べていく。
そうするとDEとの間に交点ができるのが分かるはず。それをFと名付ける。
交点なので、graphは簡単に更新できる。
平行線リストも更新する。
更にそれでBAF_p == CFE_p; #これは次のステップでやるべきだったかもしれない
BAF_p == AFD_p;
angle_lstにFの角を作る。
clockwise_lstにもFを作る。
平面上リストにも点Fを追加する。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C, F], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E, F], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D, F], [], []]
]
,
F : [
[[A], [], [C]],
[[D], [], [E]]
]
];
parallel_lines_lst := [
[[A, B], [D, F, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B]],
[D, [A], [], [C, B]],
[C, [A, D], [], [B]],
[B, [A, D, C], [], []]
]
,
F : [
[A, [], [], [D, C, E]],
[D, [A], [], [C, E]],
[C, [A, D], [], [E]],
[E, [A, D, C], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
],
F : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
[
[D, [], [], [C, E]],
[C, [D], [], [E]],
[E, [D, C], [], []]
]
,
[
[E, [], [], [A, D]],
[A, [E], [], [D]],
[D, [E, A], [], []]
]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE],
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△ACD : [CAD_p, AC, ACD_p, CD, ADC_p, AD],
△ACE : [CAE_p, AC, ACE_p, CE, AEC_p, AE]
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, B, E, D], [BAD_p, AB, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[A, B, E], [BAE_p, AB, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[A, C, D], [CAD_p, AC, ACD_p, CD, ADC_p, AD]],
[[A, C, E], [CAE_p, AC, ACE_p, CE, AEC_p, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
CAD_p + CAE_p == DAE_p;
CAD_p + BAC_p == BAD_p;
ACB_p + ACD_p == BCD_p;
ACE_p + ACD_p == DCE_p;
BAF_p == CFE_p;
BAF_p == AFD_p;
}
辺の和
AF + CF == AC; DF + EF == DE;
180°の角の和
AFD_p + CFD_p == AFC_h; AFE_p + CFE_p == AFC_h;
AFD_p + AFE_p == DFE_h; CFD_p + CFE_p == DFE_h;
angle_lstから角の和
しかしFを追加しただけなので、全部ハーフ。
三角形
△AFD
△AFE
△CFD
△CFE
そのままクラスタに
[[A, F, D], [CAD_p, AF, AFD_p, DF, ADE_p, AD]]
[[A, F, E], [CAE_p, AF, AFE_p, EF, AED_p, AE]]
[[C, F, D], [ACD_p, CF, CFD_p, DF, CDE_p, CD]]
[[C, F, E], [ACE_p, CF, CFE_p, EF, CED_p, CE]]
クラスタ割れているか 辺にFを加えて
[[A, B, E, D], [BAD_p, AB, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
[[A, B, C], [BAC_p, AB, ABC_p, BC, ACB_p, AC]],
[[A, C, D], [CAD_p, AC, ACD_p, CD, ADC_p, AD]],
[[A, C, E], [CAE_p, AC, ACE_p, CE, AEC_p, AE]]
から
DF, DFE_h, EF
AF, AFC_h, CF
なので
[[A, B, E, F, D], [BAD_p, AB, ABE_p, BE, BED_p, EF, DFE_h, DF, ADE_p, AD]],
[[A, D, F, E], [DAE_p, AD, ADE_p, DF, DFE_h, EF, AED_p, AE]],
[[C, D, F, E], [DCE_p, CD, CDE_p, DF, DFE_h, EF, CED_p, CE]]
[[A, B, C, F], [BAC_p, AB, ABC_p, BC, ACB_p, CF, AFC_h, AF]],
[[A, F, C, D], [CAD_p, AF, AFC_h, CF, ACD_p, CD, ADC_p, AD]],
[[A, F, C, E], [CAE_p, AF, AFC_h, CF, ACE_p, CE, AEC_p, AE]]
三角形定理ループを回す。けどこの環境では無理。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[C, F], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E], [], []],
[[A, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E, F], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], []],
[[D, F], [], []]
]
,
F : [
[[A], [], [C]],
[[D], [], [E]]
]
];
parallel_lines_lst := [
[[A, B], [D, F, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B]],
[D, [A], [], [C, B]],
[C, [A, D], [], [B]],
[B, [A, D, C], [], []]
]
,
F : [
[A, [], [], [D, C, E]],
[D, [A], [], [C, E]],
[C, [A, D], [], [E]],
[E, [A, D, C], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B, C]],
[C, [D], [], [E, B]],
[E, [D, C], [], [B]],
[B, [D, E, C], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D, A]],
[E, [B], [], [D, A]],
[A, [B, E], [], [D]],
[D, [B, E, A], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [B]],
[B, [C], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
],
F : [
[
[A, [], [], [D, C]],
[D, [A], [], [C]],
[C, [A, D], [], []]
]
,
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
[
[D, [], [], [C, E]],
[C, [D], [], [E]],
[E, [D, C], [], []]
]
,
[
[E, [], [], [A, D]],
[A, [E], [], [D]],
[D, [E, A], [], []]
]
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE],
△ABC : [BAC_p, AB, ABC_p, BC, ACB_p, AC],
△ACD : [CAD_p, AC, ACD_p, CD, ADC_p, AD],
△ACE : [CAE_p, AC, ACE_p, CE, AEC_p, AE],
△AFD : [CAD_p, AF, AFD_p, DF, ADE_p, AD],
△AFE : [CAE_p, AF, AFE_p, EF, AED_p, AE],
△CFD : [ACD_p, CF, CFD_p, DF, CDE_p, CD],
△CFE : [ACE_p, CF, CFE_p, EF, CED_p, CE]
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, B, E], [BAE_p, AB, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[A, B, E, F, D], [BAD_p, AB, ABE_p, BE, BED_p, EF, DFE_h, DF, ADE_p, AD]],
[[A, D, F, E], [DAE_p, AD, ADE_p, DF, DFE_h, EF, AED_p, AE]],
[[C, D, F, E], [DCE_p, CD, CDE_p, DF, DFE_h, EF, CED_p, CE]],
[[A, B, C, F], [BAC_p, AB, ABC_p, BC, ACB_p, CF, AFC_h, AF]],
[[A, F, C, D], [CAD_p, AF, AFC_h, CF, ACD_p, CD, ADC_p, AD]],
[[A, F, C, E], [CAE_p, AF, AFC_h, CF, ACE_p, CE, AEC_p, AE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
CAD_p + CAE_p == DAE_p;
CAD_p + BAC_p == BAD_p;
ACB_p + ACD_p == BCD_p;
ACE_p + ACD_p == DCE_p;
BAF_p == CFE_p;
BAF_p == AFD_p;
AF + CF == AC;
DF + EF == DE;
AFD_p + CFD_p == AFC_h;
AFE_p + CFE_p == AFC_h;
AFD_p + AFE_p == DFE_h;
CFD_p + CFE_p == DFE_h;
}
前の作図はこれで終わりなはずなので、次の作図に行く。次は線のその分だけの延長。盤面をリセットする。
これはこの方法で良いか試すためにやっているので、なるべく問題ごとが起こりそうな作図が良い。辺CEをEの方向に同じだけ伸ばしてみよう。先端にできる新しい点をFと名付ける。
まずgraphを更新する。CとEを更新して、また点Fを作る。
次にangle_lstを更新する。Eを更新して、また点Fを作る。
Eにおいては、Cが端っこにある角があれば、そのままその反対側にFを入れれば良い。
今回はそういう角を2つ作ることができたので、これは不確定要素無く記載することができたはずだ。
E : [
[
[F, [], [], [A, D, C]]
[A, [F], [], [D, C]],
[D, [A, F], [], [C]],
[C, [A, D, F], [], []]
]
,
[
[C, [], [], [B, F]],
[B, [C], [], [F]],
[F, [C, B], [], []]
]
,
[
[B, [], [], [A, D]],
[A, [B], [], [D]],
[D, [B, A], [], []]
]
]Fはどうしようかな、一つだけのEの角を作るのか、そもそも作らないのか。作ってみて、いらないと分かったら作らないことにしよう。いや作らないことにした、正の角じゃないし。
clockwise_lstに反映させる。いや、点Eにおける2つの角においてはFはその位置で良いのだけど、角BADにおいてもBとAの間にFが入るはずなんだな。
Cが途中にある角だと、Fが入らないことは確実なんだが、そもそもCが入っていない角だと、こういう場合があり得るのだな。
今回だけであれば、angle_lst→clockwise_lst→angle_lstで何とかなるんだが。まあ、今回はそういうことにしようか。
angle_lstに点Fが角が無い状態で作成されることを考えると、作業手順的には同時ということになるんだろうけど。
プログラムの上から見ていって、平行線リストへの追加は無いとして、後は平面上リストに追加する。
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F]],
[[D], [], []]
]
,
F : [
[[C, E], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B, F]],
[D, [A], [], [C, B, F]],
[C, [A, D], [], [B, F]],
[B, [A, D, C], [], [F]],
[F, [A, D, C, B], [], []]
]
,
F : [
[E, [], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[F, [], [], [A, D, C]]
[A, [F], [], [D, C]],
[D, [A, F], [], [C]],
[C, [A, D, F], [], []]
]
,
[
[C, [], [], [B, F]],
[B, [C], [], [F]],
[F, [C, B], [], []]
]
,
[
[B, [], [], [A, D, F]],
[F, [B], [], [A, D]],
[A, [B, F], [], [D]],
[D, [B, A, F], [], []]
]
]
,
F : [
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE]
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, B, E, D], [BAD_p, AB, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[A, B, E], [BAE_p, AB, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
}
プログラム(というよりデータ構造)を上から見ていって
辺の和、直線の分割による角の和
平行線リストによる角のイコール
angle_lstによる角の和の発見(本当はclockwise_lstも入れて全ての角の和を出すべき、でも今回は最初がそうじゃないから)
graphによる三角形の発見
発見した三角形をそのままクラスタに
クラスタが割れているか
三角形定理ループ
という順番で行く。
辺の和
CE + EF == CF;
角の和
AEC_p + AEF_p == CEF_h;
BEC_p + BEF_p == CEF_h;
CED_p + DEF_p == CEF_h;
平行線リストによる角のイコールは、交点がまだ発生してないので無し
三角形は、探してないが、Eから伸ばしただけなのでどうせ無い。
だから新しくクラスタとして登録する三角形は無し
またクラスタの分割も、クラスタ内で新しく点と点が繋がるということは無いはずなので、無し
三角形定理ループを回す。しかしこの環境では結果は分からない
graph := [
A : [
[[B], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F], [], []]
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F]],
[[D], [], []]
]
,
F : [
[[C, E], [], []]
]
];
parallel_lines_lst := [
[[A, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B, F]],
[D, [A], [], [C, B, F]],
[C, [A, D], [], [B, F]],
[B, [A, D, C], [], [F]],
[F, [A, D, C, B], [], []]
]
,
F : [
[E, [], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[F, [], [], [A, D, C]]
[A, [F], [], [D, C]],
[D, [A, F], [], [C]],
[C, [A, D, F], [], []]
]
,
[
[C, [], [], [B, F]],
[B, [C], [], [F]],
[F, [C, B], [], []]
]
,
[
[B, [], [], [A, D, F]],
[F, [B], [], [A, D]],
[A, [B, F], [], [D]],
[D, [B, A, F], [], []]
]
]
,
F : [
]
];
coplanar_lst := [
[A, B, C, D, E, F]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE]
];
cluster_lst := [
[[A, B, C, D], [BAD_p, AB, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, B, E, D], [BAD_p, AB, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[A, B, E], [BAE_p, AB, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
CE + EF == CF;
AEC_p + AEF_p == CEF_h;
BEC_p + BEF_p == CEF_h;
CED_p + DEF_p == CEF_h;
}
作図、分析(セットアップとほぼ同じ)と来て、ここで交点の発見をする。
本当は、分析で新しく角が明らかになったりしているのだから、今回だとEFに関して以外でも三角関数で発見する必要がある。
全ての辺を基準にして、それをすれば良い。つまり、Aに属する辺、Bに属する(A以外の)辺、Cに属する(AとB以外の)辺、という風な順番で調べていけば良い。
今回の問題では、上の3つの三角形は全て角度が分かっているし、辺を共有しているので比率でこの形は明らかになっている。更に下の三角形も、三角関数で比率で明らかになっている。
交点がAB上にできることは明らかになるだろう。
ここで一旦、流れをまとめてみた。
一旦中断して流れの整理(後から振り返る用)
「作図」
データ構造を上から見ていって
graphを更新する
平行線リストを更新する
angle_lstとclockwise_lstを更新する
平面上リストを更新する
「分析」
辺の和、直線の分割による角の和
平行線リストによって角のイコール
angle_lstとclockwise_lstによる角の和
三角形の発見
発見した三角形をそのままクラスタに
クラスタが割れているか
三角形定理ループ
「交点の発見」
Aから全ての辺で調べていく (一つの点における平均的な辺の数 ^3 * 点の数)
graphは簡単に更新できる
平行線リストを更新する
angle_lstとclockwise_lstに交点を追加する(交点の場合は他はいじる必要はない)
平面上リストにも交点を追加する
(交点が発生する辺を持つクラスタをどうするかは迷うな、次の分析のステップでやるかどうかが)
(以下、分析、交点の発見、分析、交点の発見、という風に続いていく)
再開
ではABとEFの交点Gを作図していく。
交点が発生する辺を持つクラスタをどうするかで迷うんだよな。今回は辺ABを持つクラスタだけど。やってしまおうか。
A, B → A, G, B
AB → AG, AGB_h, BG
という風に差し替える。
graph := [
A : [
[[B, G], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F], [], []] #後から発見したが、Gを入れてないというミス
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F, G]],
[[D], [], []]
]
,
F : [
[[C, E, G], [], []]
]
,
G : [
[[A], [], [B]],
[[F], [], [E, C]]
]
];
parallel_lines_lst := [
[[A, G, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B, F]],
[D, [A], [], [C, B, F]],
[C, [A, D], [], [B, F]],
[B, [A, D, C], [], [F]],
[F, [A, D, C, B], [], []]
]
,
F : [
[E, [], [], []]
]
,
G : [
[F, [], [], [A, E, B]],
[A, [F], [], [E, B]],
[E, [F, A], [], [B]],
[B, [F, A, E], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[F, [], [], [A, D, C]]
[A, [F], [], [D, C]],
[D, [A, F], [], [C]],
[C, [A, D, F], [], []]
]
,
[
[C, [], [], [B, F]],
[B, [C], [], [F]],
[F, [C, B], [], []]
]
,
[
[B, [], [], [A, D, F]],
[F, [B], [], [A, D]],
[A, [B, F], [], [D]],
[D, [B, A, F], [], []]
]
]
,
F : [
]
,
G : [
[
[F, [], [], [A, E]],
[A, [F], [], [E]],
[E, [F, A], [], []]
]
,
[
[A, [], [], [E, B]],
[E, [A], [], [B]],
[B, [A, E], [], []]
]
,
[
[E, [], [], [B, F]],
[B, [E], [], [F]],
[F, [E, B], [], []]
]
,
[
[B, [], [], [F, A]],
[F, [B], [], [A]],
[A, [B, F], [], []]
]
]
];
coplanar_lst := [
[A, B, C, D, E, F, G]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE]
];
cluster_lst := [
[[A, G, B, C, D], [BAD_p, AG, AGB_h, BG, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, G, B, E, D], [BAD_p, AG, AGB_h, BG, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[A, G, B, E], [BAE_p, AG, AGB_h, BG, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
CE + EF == CF;
AEC_p + AEF_p == CEF_h;
BEC_p + BEF_p == CEF_h;
CED_p + DEF_p == CEF_h;
}
分析する。
辺の和、直線の分割による角の和
CE + EG == CG;
AEC_p + AEG_p == CEG_h;
BEC_p + BEG_p == CEG_h;
CED_p + DEG_p == CEG_h;
AG + BG == AB;
FG + EG == EF;
FG + CG == CF;
AGF_p + BGF_p == AGB_h;
AGE_p + BGE_p == AGB_h;
AGF_p + AGE_p == EGF_h;
BGF_p + BGE_p == EGF_h;
平行線リストによって角のイコール。ぶっちゃけ手順は忘れた
DEG_p == BGE_p;
DEG_p == AGF_p;
CED_p == AGE_p;
CED_p == BGF_p;
angle_lstとclockwise_lstによる角の和。今回はGを中心にした角だけで良い
いや、交点の場合はハーフだから、そもそも登録する必要すら無いのか。
三角形の発見
△AEG
△BCG
△BEG
発見した三角形をそのままクラスタに
[[A, E, G], [BAE_p, AE, AEF_p, EG, AGE_p, AG]]
[[B, C, G], [ABC_p, BC, BCE_p, CG, BGE_p, BG]]
[[B, E, G], [ABE_p, BE, BEF_p, EG, BGE_p, BG]]
クラスタが割れているか 今回はGだけを確認すれば良いみたいだ
[A, G, B, C, D]
CG
[A, G, C, D]
[G, B, C]
[[A, G, C, D], [BAD_p, AG, AGE_p, CG, DCE_p, CD, ADC_p, AD]]
[A, G, B, E, D]
EG
[A, G, E, D]
[G, B, E]
[[A, G, E, D], [BAD_p, AG, AGE_p, EG, DEF_p, DE, ADE_p, AD]]
三角形定理ループを回す。この環境だと無理だが
graph := [
A : [
[[B, G], [], []],
[[D], [], []],
[[E], [], []]
]
,
B : [
[[A, G], [], []],
[[C], [], []],
[[E], [], []]
]
,
C : [
[[B], [], []],
[[D], [], []],
[[E, F, G], [], []] #Gを入れるのを忘れていた
]
,
D : [
[[A], [], []],
[[C], [], []],
[[E], [], []]
]
,
E : [
[[A], [], []],
[[B], [], []],
[[C], [], [F, G]],
[[D], [], []]
]
,
F : [
[[C, E, G], [], []]
]
,
G : [
[[A], [], [B]],
[[F], [], [E, C]]
]
];
parallel_lines_lst := [
[[A, G, B], [D, E]]
];
clockwise_lst := [
A : [
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
,
B : [
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
,
C : [
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
,
D : [
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
,
E : [
[A, [], [], [D, C, B, F]],
[D, [A], [], [C, B, F]],
[C, [A, D], [], [B, F]],
[B, [A, D, C], [], [F]],
[F, [A, D, C, B], [], []]
]
,
F : [
[E, [], [], []]
]
,
G : [
[F, [], [], [A, E, B]],
[A, [F], [], [E, B]],
[E, [F, A], [], [B]],
[B, [F, A, E], [], []]
]
];
angle_lst := [
A : [
[
[D, [], [], [E, B]],
[E, [D], [], [B]],
[B, [D, E], [], []]
]
]
,
B : [
[
[A, [], [], [E, C]],
[E, [A], [], [C]],
[C, [A, E], [], []]
]
]
,
C : [
[
[B, [], [], [E, D]],
[E, [B], [], [D]],
[D, [B, E], [], []]
]
]
,
D : [
[
[C, [], [], [E, A]],
[E, [C], [], [A]],
[A, [C, E], [], []]
]
]
,
E : [
[
[F, [], [], [A, D, C]]
[A, [F], [], [D, C]],
[D, [A, F], [], [C]],
[C, [A, D, F], [], []]
]
,
[
[C, [], [], [B, F]],
[B, [C], [], [F]],
[F, [C, B], [], []]
]
,
[
[B, [], [], [A, D, F]],
[F, [B], [], [A, D]],
[A, [B, F], [], [D]],
[D, [B, A, F], [], []]
]
]
,
F : [
]
,
G : [
[
[F, [], [], [A, E]],
[A, [F], [], [E]],
[E, [F, A], [], []]
]
,
[
[A, [], [], [E, B]],
[E, [A], [], [B]],
[B, [A, E], [], []]
]
,
[
[E, [], [], [B, F]],
[B, [E], [], [F]],
[F, [E, B], [], []]
]
,
[
[B, [], [], [F, A]],
[F, [B], [], [A]],
[A, [B, F], [], []]
]
]
];
coplanar_lst := [
[A, B, C, D, E, F, G]
];
triangle_lst := [
△ADE : [DAE_p, AD, ADE_p, DE, AED_p, AE],
△ABE : [BAE_p, AB, ABE_p, BE, AEB_p, AE],
△BCE : [CBE_p, BC, BCE_p, CE, BEC_p, BE],
△CDE : [DCE_p, CD, CDE_p, DE, CED_p, CE],
△AEG : [BAE_p, AE, AEF_p, EG, AGE_p, AG],
△BCG : [ABC_p, BC, BCE_p, CG, BGE_p, BG],
△BEG : [ABE_p, BE, BEF_p, EG, BGE_p, BG]
];
cluster_lst := [
[[A, G, B, C, D], [BAD_p, AG, AGB_h, BG, ABC_p, BC, BCD_p, CD, ADC_p, AD]],
[[A, G, B, E, D], [BAD_p, AG, AGB_h, BG, ABE_p, BE, BED_p, DE, ADE_p, AD]],
[[A, E, C, D], [DAE_p, AE, AEC_p, CE, DCE_p, CD, ADC_p, AD]],
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
[[A, G, B, E], [BAE_p, AG, AGB_h, BG, ABE_p, BE, AEB_p, AE]],
[[B, C, E], [CBE_p, BC, BCE_p, CE, BEC_p, BE]],
[[C, D, E], [DCE_p, CD, CDE_p, DE, CED_p, CE]],
[[A, E, G], [BAE_p, AE, AEF_p, EG, AGE_p, AG]],
[[B, C, G], [ABC_p, BC, BCE_p, CG, BGE_p, BG]],
[[B, E, G], [ABE_p, BE, BEF_p, EG, BGE_p, BG]],
[[A, G, C, D], [BAD_p, AG, AGE_p, CG, DCE_p, CD, ADC_p, AD]],
[[A, G, E, D], [BAD_p, AG, AGE_p, EG, DEF_p, DE, ADE_p, AD]]
];
always {
AB == AE;
CD == DE;
DAE == 53;
AED == 106;
CDE == 42;
BAE_p == AED_p;
DAE_p + BAE_p == BAD_p;
ABE_p + CBE_p == ABC_p;
BCE_p + DCE_p == BCD_p;
CDE_p + ADE_p == ADC_p;
AED_p + CED_p == AEC_p;
AEB_p + AED_p == BED_p;
CE + EF == CF;
AEC_p + AEF_p == CEF_h;
BEC_p + BEF_p == CEF_h;
CED_p + DEF_p == CEF_h;
CE + EG == CG;
AEC_p + AEG_p == CEG_h;
BEC_p + BEG_p == CEG_h;
CED_p + DEG_p == CEG_h;
AG + BG == AB;
FG + EG == EF;
FG + CG == CF;
AGF_p + BGF_p == AGB_h;
AGE_p + BGE_p == AGB_h;
AGF_p + AGE_p == EGF_h;
BGF_p + BGE_p == EGF_h;
DEG_p == BGE_p;
DEG_p == AGF_p;
CED_p == AGE_p;
CED_p == BGF_p;
}
じゃあリセットして、次の作図に行こうかな。
現在の二等辺三角形の作図は、底辺を基準に、角度が小さい方の辺にもう一方から新しい辺を伸ばすタイプと、角度が大きい方の辺の頂点から底辺に新しい辺を伸ばすタイプの、2種類がある。
ただ、この問題では、どちらにしてもそんなに問題は起こらないんじゃないかな、多分。
次の作図に行くことにする。クラスタを貼り合わせる。
なるべく問題が起こりやすそうな作図が良いので、△ADEのクラスタを、DEで回転させるように貼り付けよう。
新しい点をFとする。
[[A, D, E], [DAE_p, AD, ADE_p, DE, AED_p, AE]],
から
[[F, D, E], [DFE_p, DF, EDF_p, DE, DEF_p, EF]],
みたいなのを複製したい。
他は良いんだけど、angle_lstが難しい。
新しく作るFはAにおけるDとEの順番を反転させるだけで良い。しかしDとEは、例えばDの角において、Eを基準にAが時計回りで先側にあるなら、反転させたら戻った側にあるとは言えるが、それ以上言えるだろうか。
人間は、見た目や実際の角度を参考にして判断するわけだが。
こんな感じだろうか。
F : [
[
[E, [], [], [D]],
[D, [E], [], []]
]
]
D : [
[
[F, [], [C], [E, A],
[C, [], [F], [E, A]],
[E, [C, F], [], [A]],
[A, [C, E, F], [], []]
]
]
,
E : [
[
[A, [], [], [D, C, F]],
[D, [A], [], [C, F]],
[F, [A, D], [C], []],
[C, [A, D], [F], []]
]
,
[
[F, [], [C, B], []],
[C, [], [F], [B]],
[B, [C], [F], []]
]
,
[
[B, [], [], [A, D, F]],
[A, [B], [], [D, F]],
[D, [B, A], [], [F]],
[F, [B, A, F], [], []]
]
]FとDはこれで良いのだが、Eにおいては大いに問題がある。
まず、元々A・D・Cだった角には、本当はFは含まれない。それなのに、これではAとDにおいて後に存在すると確定しているようになってしまう。
最後のB・A・Dの角なんて最悪で、本当はこの角にFなんて含まれないのに、完全に確定しているかのようになってしまっている。
更に加えて、D・C・Fの角や、F・B・Aの角も、本当は新しく生まれてほしい。
clockwise_lstだったらこうなる。つまり、時計回りでEからAへは存在しない、反時計回りでDからAへは存在しない、ということになる。
D : [
[F, [], [C], [E, A]],
[C, [], [F], [E, A]],
[E, [C, F], [], [A]],
[A, [C, E, F], [], []]
]
,
E : [
[A, [], [], [D, C, B, F]],
[D, [A], [], [C, B, F]],
[F, [A, D], [C, B], []],
[C, [A, D], [F], [B]],
[B, [A, D, C], [F], []]
]いややはり、angle_lstで無くこのようにclockwise_lstで考えるべきなのだろうな。そして点EにおいてFから始まる角を生成したりする。
やっぱり、ポジティブネガティブ無しの記述法に挑戦してみたい。同じ問題で最初からそれを試してみよう。
そして駄目だったら、またここに戻ってこよう。